My friend John W. Scott makes a very perceptive takedown of a bad-science story from a few months ago. In 2015, a list of two-dozen international news sites report that leaving beds unmade helps fight dust mites; all refer back to a speculative BBC article from 2005; no confirmation or testing was ever made on the original speculation. Read more here:
2015-12-28
2015-12-21
Short Response to Flipping Classrooms
A short, possible response to the proponents of "flipping classrooms" (as though it were really a new or novel technique): Presumably we agree that students must do some kind of work outside the classroom. Then as the instructor, we might ask ourselves if we are more fulfilled by: (a) leading classroom discussions about the fundamental concepts of the discipline, or (b) serving as technicians to debug work on particular applications of those principles.
Personally, in my classes I do manage to include both aspects, but the time emphasis is more heavily on the former. If forced to pick either one or the other, then I would surely pick (a).
Personally, in my classes I do manage to include both aspects, but the time emphasis is more heavily on the former. If forced to pick either one or the other, then I would surely pick (a).
2015-12-14
Why m for Slope?
Question: Why do we use m for the slope of a line?
Personally, I always assumed that we use m because it's the numerical multiplier on the independent variable in the slope-intercept form equation y = mx +b.
Michael Sullivan's College Algebra (8th Ed., Sec. 2.3), says this as part of Exercise #133:
But others disagree. Wolfram MathWorld says the following, along with citations of particular early usages (http://mathworld.wolfram.com/Slope.html):
Personally, I always assumed that we use m because it's the numerical multiplier on the independent variable in the slope-intercept form equation y = mx +b.
Michael Sullivan's College Algebra (8th Ed., Sec. 2.3), says this as part of Exercise #133:
The accepted symbol used to denote the slope of a line is the letter m. Investigate the origin of this symbolism. Begin by consulting a French dictionary and looking up the French word monter. Write a brief essay on your findings.Of course, "monter" is a French verb which means "to climb" or "to go up".
But others disagree. Wolfram MathWorld says the following, along with citations of particular early usages (http://mathworld.wolfram.com/Slope.html):
J. Miller has undertaken a detailed study of the origin of the symbol m to denote slope. The consensus seems to be that it is not known why the letter m was chosen. One high school algebra textbook says the reason for m is unknown, but remarks that it is interesting that the French word for "to climb" is "monter." However, there is no evidence to make any such connection. In fact, Descartes, who was French, did not use m (Miller). Eves (1972) suggests "it just happened."The Math Forum at Drexel discusses this more, including a quote from J. Miller himself (http://mathforum.org/dr.math/faq/faq.terms.html):
It is not known why the letter m was chosen for slope; the choice may have been arbitrary. John Conway has suggested m could stand for "modulus of slope." One high school algebra textbook says the reason for m is unknown, but remarks that it is interesting that the French word for "to climb" is monter. However, there is no evidence to make any such connection. Descartes, who was French, did not use m. In Mathematical Circles Revisited (1971) mathematics historian Howard W. Eves suggests "it just happened."The Grammarphobia site takes up the issue likewise, citing the above, and mostly knocking down the existing theories as lacking support. They end with this witticism by Howard W. Eves (who taught at my alma mater of U. Maine, although before my time):
When lecturing before an analytic geometry class during the early part of the course... one may say: 'We designate the slope of a line by m, because the word slope starts with the letter m; I know of no better reason.'To bring things full circle, I would point out that the English word "multiplication" is spelled identically in French (and nearly the same in Latin, Italian, Spanish, Portuguese, Danish, Norwegian, and Romanian), so lacking any other historical evidence, I don't see why m for "multiplication" isn't considered as a theory in the sources above. (Compare to k for "koefficient" in Swedish textbooks, per Wolfram.)
2015-12-07
That Time I Didn't Get the Job
Here's a story that I occasionally share with my students. Back around 2001, I had left my second computer gaming job in Boston, and was still interviewing for other jobs in the industry. I had an interview at a company based in Andover, and it was mostly an hour or two in a conference room with one other staff member. I have no recollection who it was now, or if they were in engineering or production. At any rate, part of it was some standard (at the time) "code this simple thing on the whiteboard" tests of basic programming ability.
One of the questions he gave me was "write a function that takes a numeric string and converts it to the equivalent positive integer". Well, it doesn't get much more straightforward than that. I didn't really even think about it, just immediately jotted down something like the following (my C's a bit rusty now, but it was what we were working in at the time; assumes a null-terminated C string):
int parseNumber (char *s) {
int digit, sum = 0;
while (*s) {
digit = *s - '0';
sum = sum * 10 + digit;
s++;
}
return sum;
}
Well, the interviewer jumped on me, saying that's obviously wrong, because it's parsing the digits from left-to-right, whereas place values increase from right-to-left, and therefore the string must be parsed in reverse order. But that's not a problem, as I explained to him, with the way the multiples of 10 are being applied.
I stepped him through an example on the side: say the string is "1234". On the first pass, sum = 0*10+1 = 1; on the second pass, sum = 1*10+2 = 12; on the third pass, sum = 12*10+3 = 123; on the fourth pass, sum = 123*10 + 4 = 1234. Moreover, this is more efficient than the grade-school definition; in this example I've used only 4 multiplications; whereas the elementary expression of 1*10^3 + 2*10^2 + 3*10 + 4 would be using 8 multiplications (and increasingly more multiplications for larger place values; to say nothing of the expense in C of finding the back end of the string first, before knowing which place values are which).
But it was to no avail. No matter how I explained it or stepped through it, my interviewer seemed irreparably skeptical. I left and got no job offer after the fact. The thing is, part of the reason I was so confident and took zero time to think about it is because it's literally a textbook example that was given in my assembly language class in college. From George Markowsky, Real and Imaginary Machines: An Introduction to Assembly Language Programming (p. 105-106):
Postscript: Elsewhere, this can be looked at as an application of Horner's Method for evaluating polynomials, which is provably optimal in terms of minimal operations used (see texts such as: Rosen, Discrete Mathematics, 7th Edition, Sec. 3.3, Exercise 14; and Carrano, Data Abstraction & Problem Solving with C++: Walls and Mirrors, 6th Edition, Sec. 18.4.1).
However, that wasn't the only time I got static for using this textbook algorithm. As of 2019 I've shared this anecdote online at least a handful of times, and every single time, inevitably, someone argues that they wouldn't allow this solution in their codebase because it's too opaque for normal programmers to understand and maintain. (Ironically, I'm writing this postscript on the 200th anniversary of Horner's paper being presented to the Royal Society of London.)
As it turned out, I never worked in computer games or any kind of software engineering again.
One of the questions he gave me was "write a function that takes a numeric string and converts it to the equivalent positive integer". Well, it doesn't get much more straightforward than that. I didn't really even think about it, just immediately jotted down something like the following (my C's a bit rusty now, but it was what we were working in at the time; assumes a null-terminated C string):
int parseNumber (char *s) {
int digit, sum = 0;
while (*s) {
digit = *s - '0';
sum = sum * 10 + digit;
s++;
}
return sum;
}
Well, the interviewer jumped on me, saying that's obviously wrong, because it's parsing the digits from left-to-right, whereas place values increase from right-to-left, and therefore the string must be parsed in reverse order. But that's not a problem, as I explained to him, with the way the multiples of 10 are being applied.
I stepped him through an example on the side: say the string is "1234". On the first pass, sum = 0*10+1 = 1; on the second pass, sum = 1*10+2 = 12; on the third pass, sum = 12*10+3 = 123; on the fourth pass, sum = 123*10 + 4 = 1234. Moreover, this is more efficient than the grade-school definition; in this example I've used only 4 multiplications; whereas the elementary expression of 1*10^3 + 2*10^2 + 3*10 + 4 would be using 8 multiplications (and increasingly more multiplications for larger place values; to say nothing of the expense in C of finding the back end of the string first, before knowing which place values are which).
But it was to no avail. No matter how I explained it or stepped through it, my interviewer seemed irreparably skeptical. I left and got no job offer after the fact. The thing is, part of the reason I was so confident and took zero time to think about it is because it's literally a textbook example that was given in my assembly language class in college. From George Markowsky, Real and Imaginary Machines: An Introduction to Assembly Language Programming (p. 105-106):
Postscript: Elsewhere, this can be looked at as an application of Horner's Method for evaluating polynomials, which is provably optimal in terms of minimal operations used (see texts such as: Rosen, Discrete Mathematics, 7th Edition, Sec. 3.3, Exercise 14; and Carrano, Data Abstraction & Problem Solving with C++: Walls and Mirrors, 6th Edition, Sec. 18.4.1).
However, that wasn't the only time I got static for using this textbook algorithm. As of 2019 I've shared this anecdote online at least a handful of times, and every single time, inevitably, someone argues that they wouldn't allow this solution in their codebase because it's too opaque for normal programmers to understand and maintain. (Ironically, I'm writing this postscript on the 200th anniversary of Horner's paper being presented to the Royal Society of London.)
As it turned out, I never worked in computer games or any kind of software engineering again.
2015-11-30
Short Argument for Tau
Consider the use of tau (τ ~ 6.28) as a more natural unit for circular measures than pi (π ~ 3.14). I have a good colleague at school who counter-argues in this fashion: "But it's only a conversion by a factor of two, which should be trivial for us as mathematicians to deal with. And if our students can't handle that, then perhaps they shouldn't be in college."
Among the possible responses to this, here's a quick one (and specific to part of the curriculum that we teach): Scientific notation is a number written in the format \(a \cdot 10^b\). But imagine if instead we had defined it to be the format \(a \cdot 5^b\). The difference in the base is also only a factor of 2, but consider how much more complicated it is to convert between standard notation and this revised scientific notation.
Lesson: Consider your choice of basis carefully.
Among the possible responses to this, here's a quick one (and specific to part of the curriculum that we teach): Scientific notation is a number written in the format \(a \cdot 10^b\). But imagine if instead we had defined it to be the format \(a \cdot 5^b\). The difference in the base is also only a factor of 2, but consider how much more complicated it is to convert between standard notation and this revised scientific notation.
Lesson: Consider your choice of basis carefully.
2015-11-23
A Bunch of Dumb Things Journalists Say About Pi
A lovely rant by Dave Renfro, via Pat Ballew's blog, here:
2015-11-16
Joyous Excitement
Did you know that this week is the 100th anniversary of Einstein's completion of General Relativity? Specifically it was November 18, 1915 when Einstein drafted a paper that realized the final fix to his theories that would account for the previously unexplainable advance of the perihelion of Mercury. The next week he submitted this paper, "The field equations of gravitation", to the Prussian Academy of Sciences, which included what we now refer to simply as "Einstein's equations".
Einstein later recalled of this seminal moment:
And further:
(Quotes from "General Relativity" by J.J. O'Connor and E.F. Robertson at the School of Mathematics and Statistics, University of St. Andrews, Scotland).
Einstein later recalled of this seminal moment:
For a few days I was beside myself with joyous excitement.
And further:
... in all my life I have not laboured nearly so hard, and I have become imbued with great respect for mathematics, the subtler part of which I had in my simple-mindedness regarded as pure luxury until now.
(Quotes from "General Relativity" by J.J. O'Connor and E.F. Robertson at the School of Mathematics and Statistics, University of St. Andrews, Scotland).
2015-11-09
Measurement Granularity
Answering a question on StackExchange, and I came across some very nice little articles by the Six Sigma system people on Measurement System Analysis:
I like this because this issue comes up a lot in issues of the mathematics of game design: What is the most convenient and efficient scale for a particular system of measurement? And what should we be considering when we mindfully choose those units at the outset?
One key example in my D&D gaming, is that at the outset, units of encumbrance (weight carried) were ludicrously set in tenths-of-a-pound, so tracking gear carried by any characters involves adding up units in the hundreds or thousands, frequently requiring a calculator to do so. As a result, D&D encumbrance is infamous for being almost entirely unusable, and frequently discarded during play. My argument is that this is almost entirely due to an incorrect choice in measurement scale for the task -- equivalent to measuring a daily schedule in seconds, when what you really need is hours. I've recommended for a long time using the flavorfully archaic scale of "stone" weight (i.e., 14-pound units; see here), although the advantage could also be achieved by taking 5- or 10-pound units as the base. Likewise, I have a tendency to defend other Imperial units of weight as being useful in this sense (see: Human scale measurements), although I might be biased just a bit for being so steeped in D&D (further example: a league is about how far one walks in an hour, etc.).
The Six Sigma articles further show a situation where the difference in two production processes is discernible at one scale of measurement, but invisible at another incorrectly-chosen scale of measurement. See more below:
Establishing the adequacy of your measurement system using a measurement system analysis process is fundamental to measuring your own business process capability and meeting the needs of your customer (specifications). Take, for instance, cycle time measurements: It can be measured in seconds, minutes, hours, days, months, years and so on. There is an appropriate measurement scale for every customer need/specification, and it is the job of the quality professional to select the scale that is most appropriate.
I like this because this issue comes up a lot in issues of the mathematics of game design: What is the most convenient and efficient scale for a particular system of measurement? And what should we be considering when we mindfully choose those units at the outset?
One key example in my D&D gaming, is that at the outset, units of encumbrance (weight carried) were ludicrously set in tenths-of-a-pound, so tracking gear carried by any characters involves adding up units in the hundreds or thousands, frequently requiring a calculator to do so. As a result, D&D encumbrance is infamous for being almost entirely unusable, and frequently discarded during play. My argument is that this is almost entirely due to an incorrect choice in measurement scale for the task -- equivalent to measuring a daily schedule in seconds, when what you really need is hours. I've recommended for a long time using the flavorfully archaic scale of "stone" weight (i.e., 14-pound units; see here), although the advantage could also be achieved by taking 5- or 10-pound units as the base. Likewise, I have a tendency to defend other Imperial units of weight as being useful in this sense (see: Human scale measurements), although I might be biased just a bit for being so steeped in D&D (further example: a league is about how far one walks in an hour, etc.).
The Six Sigma articles further show a situation where the difference in two production processes is discernible at one scale of measurement, but invisible at another incorrectly-chosen scale of measurement. See more below:
- Measurement System Analysis Resolution, Granularity
- Proper Data Granularity Allows for Stronger Analysis
- Measurement Systems Analysis in Process Industries
2015-11-02
On Common Core
As people boil the oil and man the ramparts for this decade's education-reform efforts, I've gotten more questions recently about what I think regarding Common Core. Fortunately, I had a chance to look at it recently as part of CUNY's ongoing attempts to refine our algebra remediation and exam structure.
A few opening comments: One, this is purely in regards to the math side of things, and mostly just focused on the area of 6th-8th grade and high school Algebra I that my colleagues and I are largely involved in remediating (see the standards here: http://www.corestandards.org/Math/... and I would highlight the assertion that "Indeed, some of the highest priority content for college and career readiness comes from Grades 6-8.", Note on courses & transitions). Second, we must distinguish what Common Core specifies and what it does not: it does dictate things to know at the end of each grade level, but not how they are to be taught. In general:
I like the balanced requirement to achieve both conceptual understanding and procedural fluency ( http://www.corestandards.org/Math/Practice/). As always, my response in a lot of debates is, "you need both". And this reflects the process of presenting higher-level mathematics theorems: a careful proof, and then applications. The former guarantees correctness and understanding; the latter uses the theorem as a powerful shortcut to get work done more efficiently.
Quick example that I came across last night: "By the end of Grade 3, know from memory all products of two one-digit numbers." (http://www.corestandards.org/Math/Content/3/OA/). That's not nonsense exercise, that's a necessary tool to later understand long division, factoring, fractions, rational versus irrational numbers, estimations, the Fundamental Theorems of Arithmetic and Algebra, etc. I was happy to spot that as a case example. (And I deeply wish that we could depend on all of our college students having that skill.)
I like what I see for sample tests. Here are some examples from the nation-wide PARCC consortium (by Pearson, of course; http://parcc.pearson.com/practice-tests/math/): I'm looking at the 7th- and 8th-grade and Algebra I tests. They all come in two parts: Part I, short questions, multiple-choice, with no calculators allowed. Part II, more sophisticated questions, short-answer (not multiple choice), with calculators allowed. I think that's great: you need both.
New York State writes their own Common Core tests instead of using PARCC, at least at the high school level (http://www.nysedregents.org/): here I'm looking mostly at Algebra I (http://www.nysedregents.org/algebraone/). Again, a nice pattern of one part multiple-choice, the other part short-answer. I wish we could do that in our system. Now, the NYS Algebra I test is all-graphing-calculator mandatory, which sets my teeth on edge a bit compared to the PARCC tests. Maybe I could live with that as long as students have confirmed mental mastery at the 7th- and 8th-grade level (not that I can confirm that they do). Even the grading rubric shown here for NYS looks fine to me (approximately half-credit for calculation, and half-credit for conceptual understanding and approach on any problem; that's pretty close to what I've evolved to do in my own classes).
In summary: Pretty great stuff as far as published standards and test questions (at least for 7th-8th grade math and Algebra I).
Most teachers in grades K-6, and even 7-8 in some places (note that's specifically the key grades highlighted above for "some of the highest priority content for college and career readiness") are not mathematics specialists. In fact, U.S. education school entrants are perennially the very weakest of all incoming college students in proficiency and attitude towards math (also: here). If the teachers at these levels fundamentally don't understand math themselves -- don't understand the later algebra and STEM work that it prepares them for -- then I have a really tough time seeing how they can understand the Common Core requirements, or effectively select and implement appropriate mathematical curriculum for their classrooms. Sometimes I refer to students at this level as having "anti-knowledge" -- and I find that it's much easier to instruct a student who has never heard of algebra ever (which sometimes happens for graduates of certain religious programs) than it is to deconstruct and repair incorrect the conceptual frameworks of students with many years of broken instruction.
Before I go on: The best solution to this would be to massively increase salary and benefits for all public-school teachers, and implement top-notch rigorous requirements for entry to education programs (as done in other top-performing nations). A second-best solution, which is probably more feasible in the near-term, would be to place mathematics-specialist teachers in all grades K-12.
The other key problem I see is: how are the test scores generated? We already know that in many places students take tests, and then the test scores are arbitrarily inflated or scaled by the state institutions, manipulating them to guarantee some particular high percentage is deemed "passing" (regardless of actual proficiency, for political purposes). For example, the conversion chart for NYS Algebra I Common Core raw scores to final scores for this past August is shown below (from NYS regents link above):
Now, this is a test that had a maximum total 86 possible points scored. If we linearly converted this to a percentage, we would just multiply any score by 100/86 = 1.16; it would add 14 points at the top of the scale, about 7 points at the middle, and 0 points at the bottom. But that's not what we see here -- it's a nonlinear scaling from raw to final. The top adds 14 points, but in the middle it adds 30 or more points in the raw range from 13 to 40.
The final range is 0 to 100, allowing you to think it might be a percentage, but it's not. If we consider 60% be minimal normal passing at a test, for this test that would occur at the 52-point raw score mark; but that gets scaled to a 73 final score, which usually means a middle-C grade. Looking at the 5 performance levels (more-or-less equivalent to A- through F- letter grades): A performance level of "3" is achieved with a raw score of just 30, which is only 30/86 = 35% of the available points on the test. A performance level of "2" is achieved with a raw score of only 20, that is, 20/86 = 23% of the available points on the test. And these low levels (near random-guessing) are considered acceptable for awards of a high school diploma (www.p12.nysed.gov/assessment/reports/commoncore/tr-a1-ela.pdf, p. 19):
In summary: While the publicized standards and exam formats look fine to me, the devil is in the details. On the input end, actual curriculum and instruction are left as undefined behavior in the hands of primary-school teachers who are not specialists, and rarely empowered, and frequently the very weakest of all professionals in math skills and understanding. And on the output end, grading scales can be manipulated arbitrarily to show any desired passing rate, almost entirely disconnected from the actual level of mastery demonstrated in a cohort of students. So I fear that almost any number of students can go through a system like that and not actual meet the published Common Core standards to be ready for work in college or a career.
A few opening comments: One, this is purely in regards to the math side of things, and mostly just focused on the area of 6th-8th grade and high school Algebra I that my colleagues and I are largely involved in remediating (see the standards here: http://www.corestandards.org/Math/... and I would highlight the assertion that "Indeed, some of the highest priority content for college and career readiness comes from Grades 6-8.", Note on courses & transitions). Second, we must distinguish what Common Core specifies and what it does not: it does dictate things to know at the end of each grade level, but not how they are to be taught. In general:
The standards establish what students need to learn, but they do not dictate how teachers should teach. Teachers will devise their own lesson plans and curriculum, and tailor their instruction to the individual needs of the students in their classrooms. (Frequently Asked Questions: What guidance do the Common Core Standards provide to teachers?)Specifically in regards to math:
The standards themselves do not dictate curriculum, pedagogy, or delivery of content. (Note on courses & transitions)So this foreshadows a two-part answer:
(1) I think the standards look great.
Everything that I've seen in the standards themselves looks smart, rigorous, challenging, core to the subject, and pretty much indispensable to a traditional college curriculum in calculus, statistics, computer programming, and other STEM pursuits. I encourage you to read them at the link above. It includes pretty much everything in a standard algebra sequence for the last few centuries or so.I like the balanced requirement to achieve both conceptual understanding and procedural fluency ( http://www.corestandards.org/Math/Practice/). As always, my response in a lot of debates is, "you need both". And this reflects the process of presenting higher-level mathematics theorems: a careful proof, and then applications. The former guarantees correctness and understanding; the latter uses the theorem as a powerful shortcut to get work done more efficiently.
Quick example that I came across last night: "By the end of Grade 3, know from memory all products of two one-digit numbers." (http://www.corestandards.org/Math/Content/3/OA/). That's not nonsense exercise, that's a necessary tool to later understand long division, factoring, fractions, rational versus irrational numbers, estimations, the Fundamental Theorems of Arithmetic and Algebra, etc. I was happy to spot that as a case example. (And I deeply wish that we could depend on all of our college students having that skill.)
I like what I see for sample tests. Here are some examples from the nation-wide PARCC consortium (by Pearson, of course; http://parcc.pearson.com/practice-tests/math/): I'm looking at the 7th- and 8th-grade and Algebra I tests. They all come in two parts: Part I, short questions, multiple-choice, with no calculators allowed. Part II, more sophisticated questions, short-answer (not multiple choice), with calculators allowed. I think that's great: you need both.
New York State writes their own Common Core tests instead of using PARCC, at least at the high school level (http://www.nysedregents.org/): here I'm looking mostly at Algebra I (http://www.nysedregents.org/algebraone/). Again, a nice pattern of one part multiple-choice, the other part short-answer. I wish we could do that in our system. Now, the NYS Algebra I test is all-graphing-calculator mandatory, which sets my teeth on edge a bit compared to the PARCC tests. Maybe I could live with that as long as students have confirmed mental mastery at the 7th- and 8th-grade level (not that I can confirm that they do). Even the grading rubric shown here for NYS looks fine to me (approximately half-credit for calculation, and half-credit for conceptual understanding and approach on any problem; that's pretty close to what I've evolved to do in my own classes).
In summary: Pretty great stuff as far as published standards and test questions (at least for 7th-8th grade math and Algebra I).
(2) The implementation is possibly suspect.
Having established rigorous standards and examinations, these don't solve some of the endemic problems in our primary education system. Granted that "Teachers will devise their own lesson plans and curriculum, and tailor their instruction to the individual needs of the students in their classrooms." (above):Most teachers in grades K-6, and even 7-8 in some places (note that's specifically the key grades highlighted above for "some of the highest priority content for college and career readiness") are not mathematics specialists. In fact, U.S. education school entrants are perennially the very weakest of all incoming college students in proficiency and attitude towards math (also: here). If the teachers at these levels fundamentally don't understand math themselves -- don't understand the later algebra and STEM work that it prepares them for -- then I have a really tough time seeing how they can understand the Common Core requirements, or effectively select and implement appropriate mathematical curriculum for their classrooms. Sometimes I refer to students at this level as having "anti-knowledge" -- and I find that it's much easier to instruct a student who has never heard of algebra ever (which sometimes happens for graduates of certain religious programs) than it is to deconstruct and repair incorrect the conceptual frameworks of students with many years of broken instruction.
Before I go on: The best solution to this would be to massively increase salary and benefits for all public-school teachers, and implement top-notch rigorous requirements for entry to education programs (as done in other top-performing nations). A second-best solution, which is probably more feasible in the near-term, would be to place mathematics-specialist teachers in all grades K-12.
The other key problem I see is: how are the test scores generated? We already know that in many places students take tests, and then the test scores are arbitrarily inflated or scaled by the state institutions, manipulating them to guarantee some particular high percentage is deemed "passing" (regardless of actual proficiency, for political purposes). For example, the conversion chart for NYS Algebra I Common Core raw scores to final scores for this past August is shown below (from NYS regents link above):
Now, this is a test that had a maximum total 86 possible points scored. If we linearly converted this to a percentage, we would just multiply any score by 100/86 = 1.16; it would add 14 points at the top of the scale, about 7 points at the middle, and 0 points at the bottom. But that's not what we see here -- it's a nonlinear scaling from raw to final. The top adds 14 points, but in the middle it adds 30 or more points in the raw range from 13 to 40.
The final range is 0 to 100, allowing you to think it might be a percentage, but it's not. If we consider 60% be minimal normal passing at a test, for this test that would occur at the 52-point raw score mark; but that gets scaled to a 73 final score, which usually means a middle-C grade. Looking at the 5 performance levels (more-or-less equivalent to A- through F- letter grades): A performance level of "3" is achieved with a raw score of just 30, which is only 30/86 = 35% of the available points on the test. A performance level of "2" is achieved with a raw score of only 20, that is, 20/86 = 23% of the available points on the test. And these low levels (near random-guessing) are considered acceptable for awards of a high school diploma (www.p12.nysed.gov/assessment/reports/commoncore/tr-a1-ela.pdf, p. 19):
In summary: While the publicized standards and exam formats look fine to me, the devil is in the details. On the input end, actual curriculum and instruction are left as undefined behavior in the hands of primary-school teachers who are not specialists, and rarely empowered, and frequently the very weakest of all professionals in math skills and understanding. And on the output end, grading scales can be manipulated arbitrarily to show any desired passing rate, almost entirely disconnected from the actual level of mastery demonstrated in a cohort of students. So I fear that almost any number of students can go through a system like that and not actual meet the published Common Core standards to be ready for work in college or a career.
2015-10-26
Double Factorial Table
The double factorial is the product of a number and every second natural number less than itself. That is:
Presentation of the values for double factorials is usually split up into separate even- and odd- sequences. Instead, I wanted to see the sequence all together, as below:
\(n!! = \prod_{k = 0}^{ \lceil n/2 \rceil - 1} (n - 2k) = n(n-2)(n-4)...\)
Presentation of the values for double factorials is usually split up into separate even- and odd- sequences. Instead, I wanted to see the sequence all together, as below:
2015-10-19
Geometry Formulas in Tau
Here's a modified a geometry formula sheet so all the presentations of circular shapes are in terms of tau (not pi); tack it to your wall and see if anybody spots the difference.
(Original sheet here.)
(Original sheet here.)
2015-10-12
On Zeration
In my post last week on hyperoperations, I didn't talk much about the operation under addition, the zero-th operation in the hierarchy, which many refer to as "zeration". There is a surprising amount of disagreement about exactly how zeration should be defined.
The standard Peano axioms defining the natural numbers stipulate a single operation called the "successor". This is commonly written S(n), which indicates the next natural number after n. Later on, addition is defined in terms of repeated successor operations, and so forth.
The traditional definition of zeration, per Goodstein, is: \(H_0(a, b) = b + 1\). Now when I first saw this, I was surprised and taken aback. All the other operations start with \(a\) as a "base", and then effectively apply some simpler operation \(b\) times, so it seems odd to start with the \(b\) and just add one to it. (If anything my expectation would have been to take \(a+1\), but that doesn't satisfy the regular recursive definition of \(H_n\) when you try to construct addition.)
As it turns out, when you get to this basic level, you're doomed to lose many of the regular properties of the operations hierarchy. So there's nothing to do but start arguing about which properties to prioritize as "most fundamental" when constructing the definition.
Here are some points in favor of the standard definition \(b+1\): (1) It does satisfy the recursive formula that repeated applications are equivalent to addition (\(H_1\)). (2) It does looking passingly like counting by 1, i.e., the Peano "successor" operation. (3) It shares the key identity that \(H_n(a, 0) = 1\), for all \(n \ge 3\). (4) Since it is an elementary operation (addition, really), it can be extended from natural numbers to all real and complex numbers in a fashion which is analytic (infinitely differentiable).
But here are some points against the standard definition (1) It is not "really" a binary operator like the rest of the hierarchy, in that it totally ignores the first parameter \(a\). (2) Because of its ignoring \(a\), it's not commutative like the other low-level operations n = 1 or 2 (yet like them it is still associative and distributive, or as I sometimes say, collective of the next higher operation). (3) For the same reason, it has no identity element (no way to recover the value \(a\), unique among the entire hyperoperations hierarchy). (4) It's the only hyperoperation which doesn't need a special base case for when \(b = 0\). (5) I might turn around favorable point #3 above and call it weird and unfavorable, in that it is misaligned in this way with operations n = 1 and 2, and it's the only case of one of the key identities being added at a lower level instead of being lost. See how weird that looks below?
So as a result, a variety of alternative definitions have been put forward. I think my favorite is \(H_0(a, b) = max(a, b) + 1\). Again, this looks a lot like counting; I might possibly explain it to a young student as "count one more than the largest number you've seen before". Points in favor: (1) Repeated applications are again the same as addition. (2) It is truly a binary operation. (3) It is commutative, and thus completes the trifecta of commutativity, association, and distribution/collection being true for all operations \(n < 3\). (4) It does have an identity element, in \(b = 0\). (5) It maintains the pattern of losing more of the high-level identities, and in fact perfects the situation in that none of the five identities hold for this zeration (all "no's" in the modified table above for \(n = 0\)). Points against: (1) It isn't exactly the same as the unary Peano successor function. (2) It's non-differentiable, and therefore cannot be extended to an analytic function over the fields of real or complex numbers.
There are vocal proponents of related possible re-definition: \(H_0(a, b) = max(a, b) + 1\) if a ≠ b, \(a + 2\) if a = b. Advantage here is that it matches some identities in other operations, like \(H_n(a, a) = H_{n+1}(a, 2)\) and \(H_n(2, 2) = 4\), but I'm less impressed by specific magic numbers like that (as compared to having commutativity and the pattern of actually losing more identities). Disadvantage is obviously that the possibility of adding 2 in the \(a+2\) case gets us even further away from the simple Peano successor function.
And then some people want to establish commutativity so badly that they assert this: \(H_0(a, b) = ln(e^a + e^b)\). That does get you commutativity, but at that point we're so far away from simple counting in natural numbers that I don't even want to think about it.
Final thought: While most people interpret the standard definition of zeration, \(H_0(a, b) = b + 1\) as "counting 1 more place from b", it makes more sense to my brain to turn that around and say that we are "counting b places from 1". That is, ignoring the \(a\) parameter, start at the number 1 and apply the successor function repeatedly b times: \(S(S(S(...S(1))))\), with the \(S\) function appearing \(b\) times. This feels more like "basic" Peano counting, it maintains the sense of \(b\) being the number of times some simpler operation is applied, and it avoids defining zeration in terms of the higher operation of addition. And then you also need to stipulate a special base case for \(b = 0\), like all the other hyperoperations, namely \(H_0(a, 0) = 1\).
So maybe the standard definition is the best we can do, and the closest expression of what Peano successor'ing in natural numbers (counting) really indicates. Perhaps we can't really have a "true" binary operator at level \(H_0\), at a point when we haven't even discovered what the number "2" is yet.
P.S. Can we consider defining an operation one level even lower, perhaps \(H_{-1}(a, b) = 1\) which ignores both parameters, just returns the natural number 1, and loses every single one of the regular properties of hyperoperations (including recursivity in the next one up)?
The standard Peano axioms defining the natural numbers stipulate a single operation called the "successor". This is commonly written S(n), which indicates the next natural number after n. Later on, addition is defined in terms of repeated successor operations, and so forth.
The traditional definition of zeration, per Goodstein, is: \(H_0(a, b) = b + 1\). Now when I first saw this, I was surprised and taken aback. All the other operations start with \(a\) as a "base", and then effectively apply some simpler operation \(b\) times, so it seems odd to start with the \(b\) and just add one to it. (If anything my expectation would have been to take \(a+1\), but that doesn't satisfy the regular recursive definition of \(H_n\) when you try to construct addition.)
As it turns out, when you get to this basic level, you're doomed to lose many of the regular properties of the operations hierarchy. So there's nothing to do but start arguing about which properties to prioritize as "most fundamental" when constructing the definition.
Here are some points in favor of the standard definition \(b+1\): (1) It does satisfy the recursive formula that repeated applications are equivalent to addition (\(H_1\)). (2) It does looking passingly like counting by 1, i.e., the Peano "successor" operation. (3) It shares the key identity that \(H_n(a, 0) = 1\), for all \(n \ge 3\). (4) Since it is an elementary operation (addition, really), it can be extended from natural numbers to all real and complex numbers in a fashion which is analytic (infinitely differentiable).
But here are some points against the standard definition (1) It is not "really" a binary operator like the rest of the hierarchy, in that it totally ignores the first parameter \(a\). (2) Because of its ignoring \(a\), it's not commutative like the other low-level operations n = 1 or 2 (yet like them it is still associative and distributive, or as I sometimes say, collective of the next higher operation). (3) For the same reason, it has no identity element (no way to recover the value \(a\), unique among the entire hyperoperations hierarchy). (4) It's the only hyperoperation which doesn't need a special base case for when \(b = 0\). (5) I might turn around favorable point #3 above and call it weird and unfavorable, in that it is misaligned in this way with operations n = 1 and 2, and it's the only case of one of the key identities being added at a lower level instead of being lost. See how weird that looks below?
So as a result, a variety of alternative definitions have been put forward. I think my favorite is \(H_0(a, b) = max(a, b) + 1\). Again, this looks a lot like counting; I might possibly explain it to a young student as "count one more than the largest number you've seen before". Points in favor: (1) Repeated applications are again the same as addition. (2) It is truly a binary operation. (3) It is commutative, and thus completes the trifecta of commutativity, association, and distribution/collection being true for all operations \(n < 3\). (4) It does have an identity element, in \(b = 0\). (5) It maintains the pattern of losing more of the high-level identities, and in fact perfects the situation in that none of the five identities hold for this zeration (all "no's" in the modified table above for \(n = 0\)). Points against: (1) It isn't exactly the same as the unary Peano successor function. (2) It's non-differentiable, and therefore cannot be extended to an analytic function over the fields of real or complex numbers.
There are vocal proponents of related possible re-definition: \(H_0(a, b) = max(a, b) + 1\) if a ≠ b, \(a + 2\) if a = b. Advantage here is that it matches some identities in other operations, like \(H_n(a, a) = H_{n+1}(a, 2)\) and \(H_n(2, 2) = 4\), but I'm less impressed by specific magic numbers like that (as compared to having commutativity and the pattern of actually losing more identities). Disadvantage is obviously that the possibility of adding 2 in the \(a+2\) case gets us even further away from the simple Peano successor function.
And then some people want to establish commutativity so badly that they assert this: \(H_0(a, b) = ln(e^a + e^b)\). That does get you commutativity, but at that point we're so far away from simple counting in natural numbers that I don't even want to think about it.
Final thought: While most people interpret the standard definition of zeration, \(H_0(a, b) = b + 1\) as "counting 1 more place from b", it makes more sense to my brain to turn that around and say that we are "counting b places from 1". That is, ignoring the \(a\) parameter, start at the number 1 and apply the successor function repeatedly b times: \(S(S(S(...S(1))))\), with the \(S\) function appearing \(b\) times. This feels more like "basic" Peano counting, it maintains the sense of \(b\) being the number of times some simpler operation is applied, and it avoids defining zeration in terms of the higher operation of addition. And then you also need to stipulate a special base case for \(b = 0\), like all the other hyperoperations, namely \(H_0(a, 0) = 1\).
So maybe the standard definition is the best we can do, and the closest expression of what Peano successor'ing in natural numbers (counting) really indicates. Perhaps we can't really have a "true" binary operator at level \(H_0\), at a point when we haven't even discovered what the number "2" is yet.
P.S. Can we consider defining an operation one level even lower, perhaps \(H_{-1}(a, b) = 1\) which ignores both parameters, just returns the natural number 1, and loses every single one of the regular properties of hyperoperations (including recursivity in the next one up)?
2015-10-05
On Hyperoperations
Consider the basic operations: Repeated counting is addition; repeated addition is multiplication; repeated multiplication is exponentiation. Hyperoperations are the idea of generally extending this sequence. This was first proposed as such, in a passing comment, by R. L. Goodstein in an article to the Journal of Symbolic Logic, "Transfinite Ordinals in Recursive Number Theory" (1947):
At this point, there are a lot of different ways of denoting these operations. There's \(H_n\) notation. There's the Knuth up-arrow notation. There's box notation and bracket notation. The Ackerman function means almost the same thing. Conway's chained arrow notation can be used to show them. Some people concisely symbolize the zero-th level operation (under addition) as \(a \circ b\), and the fourth operation (above exponentiation) as \(a \# b\). Wikipedia reiterates Goodstein's original definition like so, for \(H_n (a,b): (\mathbb N_0)^3 \to \mathbb N_0\):
Let's use Goodstein's suggested names for the levels above exponentiation. Repeated exponentiation is tetration; repeated tetration is pentation; repeated pentation is hexation; and so forth. Since I don't see them anywhere else online, below you'll find some partial hyperproduct tables for these next-level operations (and ODS spreadsheet here). Of course, the values get large very fast; you'll see some entries in scientific notation, and then "#NUM!" indicates a place where my spreadsheet could no longer handle the value (that is, something greater than \(1 \times 10^{308}\)).
From this point forward, the hyperoperation tables look passingly similar in this limited view. You have some fixed values in the first two rows and columns; the 2-by-2 result is eternally 4; and everything other than that is so astronomically huge that you can't even usefully write it in scientific notation. Here are some identities suggested above that we can prove pretty easily for all hyperoperations \(n > 3\):
Now, to connect up to my post last week, recall the basic properties of real numbers taken as axiomatic at the start of most algebra and analysis classes. Addition and multiplication (n = 1 and 2) are commutative and associative; but exponents are not, and neither are any of the higher operations.
Finally consider the general case of distribution, what in my algebra classes I summarize as the "General Distribution Rule" (Principle #2 here). Or perhaps based on last week's observation I might suggest it could be better phrased as "collecting terms of the next higher operation", like \(ac + bc = (a+b)c\) and \(a^c \cdot b^c = (a \cdot b)^c\), or in the general hyperoperational form:
Well, just like commutativity and associativity, distribution in this general form also holds for n = 1 and 2, but fails for higher operations. Here's the first counterexample, using \(a \uparrow b\) for exponents (\(H_3\)), and \(a \# b\) for tetration (\(H_4\)):
Likewise, what I call the "Fundamental Rules of Exponents" (Principle #1 above, or also here) works only for levels \(n \le 3\), and fails to be meaningful at higher levels of hyperoperation.
At this point, there are a lot of different ways of denoting these operations. There's \(H_n\) notation. There's the Knuth up-arrow notation. There's box notation and bracket notation. The Ackerman function means almost the same thing. Conway's chained arrow notation can be used to show them. Some people concisely symbolize the zero-th level operation (under addition) as \(a \circ b\), and the fourth operation (above exponentiation) as \(a \# b\). Wikipedia reiterates Goodstein's original definition like so, for \(H_n (a,b): (\mathbb N_0)^3 \to \mathbb N_0\):
Let's use Goodstein's suggested names for the levels above exponentiation. Repeated exponentiation is tetration; repeated tetration is pentation; repeated pentation is hexation; and so forth. Since I don't see them anywhere else online, below you'll find some partial hyperproduct tables for these next-level operations (and ODS spreadsheet here). Of course, the values get large very fast; you'll see some entries in scientific notation, and then "#NUM!" indicates a place where my spreadsheet could no longer handle the value (that is, something greater than \(1 \times 10^{308}\)).
From this point forward, the hyperoperation tables look passingly similar in this limited view. You have some fixed values in the first two rows and columns; the 2-by-2 result is eternally 4; and everything other than that is so astronomically huge that you can't even usefully write it in scientific notation. Here are some identities suggested above that we can prove pretty easily for all hyperoperations \(n > 3\):
- \(H_n(a, 0) = 1\) (by definition)
- \(H_n(a, 1) = a\)
- \(H_n(0, b) = \) 0 if b odd, 1 if b even
- \(H_n(1, b) = 1\)
- \(H_n(2, 2) = 4\)
Now, to connect up to my post last week, recall the basic properties of real numbers taken as axiomatic at the start of most algebra and analysis classes. Addition and multiplication (n = 1 and 2) are commutative and associative; but exponents are not, and neither are any of the higher operations.
Finally consider the general case of distribution, what in my algebra classes I summarize as the "General Distribution Rule" (Principle #2 here). Or perhaps based on last week's observation I might suggest it could be better phrased as "collecting terms of the next higher operation", like \(ac + bc = (a+b)c\) and \(a^c \cdot b^c = (a \cdot b)^c\), or in the general hyperoperational form:
\(H_n(H_{n+1}(a, c), H_{n+1}(b, c)) = H_{n+1}(H_n(a, b), c)\)
Well, just like commutativity and associativity, distribution in this general form also holds for n = 1 and 2, but fails for higher operations. Here's the first counterexample, using \(a \uparrow b\) for exponents (\(H_3\)), and \(a \# b\) for tetration (\(H_4\)):
\((2\#2)\uparrow (0\#2) = 4 \uparrow 1 = 4\), but
\((2 \uparrow 0)\#2 = 1 \# 2 = 1\).
Likewise, what I call the "Fundamental Rules of Exponents" (Principle #1 above, or also here) works only for levels \(n \le 3\), and fails to be meaningful at higher levels of hyperoperation.
2015-09-28
Why Is Distribution Prioritized Over Combining?
So I've come up with this question that's been bothering me for weeks,and I've been searching and asking everyone and everywhere that I can. I suspect that it may have no answer. The question is this:
In dimensional analysis, some call the idea of only adding or comparing like units the "Great Principle of Similitude". Which provides some of my motivation for wishing that we would start with this ("combining") and then derive distribution (using commutativity a few times). Note that this phrase is in many places erroneously attributed to Newton; in truth the earliest documented usage of the phrase is by Rayleigh in a letter to Nature (No. 2368, Vol. 95; March 18, 1915). I could probably write a whole post just on the hunt for this quote. Big thanks to Juan Santiago who teaches a class by that name at Stanford (link) for helping me track down the article.
The Math Forum at Drexel discusses some history of the names of the basic properties. The best that Doctor Peterson can track down is that terms such as "distribution" were first used in the late 1700's to 1800's (starting in French in a memoir by Francois Joseph Servois). No commentary on a reason for why this was picked over alternative formulations. But perhaps the fact that the original discussion was in terms of functions (not binary operators) provides a clue. (For the full French text, see here and search "commutative and distributive").
Here's me asking the question at the StackExchange Mathematics site. Unfortunately, most commentators considered it to be uninteresting. When it got no responses, I cross-posted to the Mathematics Educators site -- which is apparently a huge faux pas, and immediately got it down-moderated into oblivion. The only relevant answer to date was from Benjamin Dickman, who pointed to a very nice quote from Euclid: when he states a similar property in geometric terms (area of a rectangle versus the sum of it being sliced up), it happens to be in the same order as we present the distribution property. But still no word on any reason why it should be in that order and not the reverse.
Observations from a few textbooks that I have lying around:
Another thought is that while you can point to distribution as justifying the standard long-multiplication process (across decimal place value), the interior additions are implied and not explicit, and so they don't really serve to develop intuition in the same way that simple unit addition does.
Therefore, I find myself fantasizing about the following. Write a slightly nonstandard algebra textbook that starts by assuming commutativity, association, and the combining-like-terms-property (and shortly after deriving the distribution property). Perhaps for a better name it could be called "collection of like multiplications inside addition", or something like that.
Do you think this would be a better set of axioms for a basic algebra class? Can you think of a solid historical or pedagogical reason why the name and presentation were not the other way around, like this? Likely some more on this later.
Consider the properties of real numbers that we take for granted at the start of an algebra or analysis class (commutativity, association, and distribution of multiplying over addition). Granted that the last one, distribution (the transformation \(a(b+c) = ab + ac\)), is effectively equivalent to what we might call "combining like terms" (the transformation \(ax + bx = (a+b)x\)). It seems like the latter is more fundamental and easier to intuit as an axiom, since it resembles simple addition of units (e.g., 3 feet + 5 feet = 8 feet). So historically and/or pedagogically, what was the reason choosing the name and order we have ("distribution", \(a(b+c)=ab+ac\)), instead of the other option ("combining", \(ax+bx = (a+b)x\)) for the starting axiom?I suspect now that there simply isn't any reason that we can document. Some expansion on the problem:
In dimensional analysis, some call the idea of only adding or comparing like units the "Great Principle of Similitude". Which provides some of my motivation for wishing that we would start with this ("combining") and then derive distribution (using commutativity a few times). Note that this phrase is in many places erroneously attributed to Newton; in truth the earliest documented usage of the phrase is by Rayleigh in a letter to Nature (No. 2368, Vol. 95; March 18, 1915). I could probably write a whole post just on the hunt for this quote. Big thanks to Juan Santiago who teaches a class by that name at Stanford (link) for helping me track down the article.
The Math Forum at Drexel discusses some history of the names of the basic properties. The best that Doctor Peterson can track down is that terms such as "distribution" were first used in the late 1700's to 1800's (starting in French in a memoir by Francois Joseph Servois). No commentary on a reason for why this was picked over alternative formulations. But perhaps the fact that the original discussion was in terms of functions (not binary operators) provides a clue. (For the full French text, see here and search "commutative and distributive").
Here's me asking the question at the StackExchange Mathematics site. Unfortunately, most commentators considered it to be uninteresting. When it got no responses, I cross-posted to the Mathematics Educators site -- which is apparently a huge faux pas, and immediately got it down-moderated into oblivion. The only relevant answer to date was from Benjamin Dickman, who pointed to a very nice quote from Euclid: when he states a similar property in geometric terms (area of a rectangle versus the sum of it being sliced up), it happens to be in the same order as we present the distribution property. But still no word on any reason why it should be in that order and not the reverse.
Observations from a few textbooks that I have lying around:
- Rietz and Crathorne, Introductory College Algebra (1933). Article 4 shows combining like terms, and asserts that's justified by the associative law (which is nonsensical). The distributive property isn't presented until later, in Article 8.
- Martin-Gay, Prealgebra & Introductory Algebra. In the purely numerical prealgebra section, this first shows up as distribution among numbers (Sec 1.5). But the first time it appears in the algebra section with variables it is in fact written and used for combining like terms (Sec 3.1: \(ac + bc = (a+b)c\), although still called the "distributive property"). Combining like terms is actually done even earlier than that on an intuitive basis (see Sec. 2.6, Example 4). Only later is the property presented and used to remove parentheses from variable expressions.
- Bittinger's Intermediate Algebra shows standard distribution, followed immediately by use for combining like terms. Sullivan's Algebra & Trigonometry does the same.
Another thought is that while you can point to distribution as justifying the standard long-multiplication process (across decimal place value), the interior additions are implied and not explicit, and so they don't really serve to develop intuition in the same way that simple unit addition does.
Therefore, I find myself fantasizing about the following. Write a slightly nonstandard algebra textbook that starts by assuming commutativity, association, and the combining-like-terms-property (and shortly after deriving the distribution property). Perhaps for a better name it could be called "collection of like multiplications inside addition", or something like that.
Do you think this would be a better set of axioms for a basic algebra class? Can you think of a solid historical or pedagogical reason why the name and presentation were not the other way around, like this? Likely some more on this later.
2015-09-21
Rational Numbers and Randomized Digits
Here's a quick thought experiment to develop intuition about the cardinality of rational versus irrational decimal numbers. We know that any rational number (a/b with integer a, b and b ≠ 0) has a decimal expansion that either terminates or repeats (and terminating is itself equivalent to ending with a repeating block of all 0's).
Consider randomizing decimal digits in an infinite string (say, by using a standard d10 from a roleplaying game, shown above). How likely does it seem that at any point you'll start rolling repeated 0's, and nothing but 0's, until the end of time? It's obviously diminishingly unlikely, so effectively impossible that you'll roll a terminating decimal. Alternatively, how probable does it seem that you'll roll some particular block of digits, and then repeat them in exactly the same order, and keep doing so without fail an infinite number of times? Again, it seems effectively impossible.
So this intuitively shows that if you pick any real number "at random" (in this case, generating random decimal digits one at a time), it's effectively certain that you'll produce an irrational number. The proportion of rational numbers can be seen to be practically negligible compared to the preponderance of irrationals.
Consider randomizing decimal digits in an infinite string (say, by using a standard d10 from a roleplaying game, shown above). How likely does it seem that at any point you'll start rolling repeated 0's, and nothing but 0's, until the end of time? It's obviously diminishingly unlikely, so effectively impossible that you'll roll a terminating decimal. Alternatively, how probable does it seem that you'll roll some particular block of digits, and then repeat them in exactly the same order, and keep doing so without fail an infinite number of times? Again, it seems effectively impossible.
So this intuitively shows that if you pick any real number "at random" (in this case, generating random decimal digits one at a time), it's effectively certain that you'll produce an irrational number. The proportion of rational numbers can be seen to be practically negligible compared to the preponderance of irrationals.
2015-09-14
Algebra for Cryptography
Cryptography researcher Victor Shoup recently gave a talk at the Simons Institute at Berkeley. Richard Lipton quotes him in one of his interesting observations about cryptography:
He also made another point: For the basic type of systems under discussion, he averred that the mathematics needed to describe and understand them was essentially high school algebra. Or as he said, “at least high school algebra outside the US.”Quoted here.
2015-09-07
The MOOC Revolution that Wasn't
Three years ago I wrote a review of "Udacity Statistics 101" that went
semi-viral, finding the MOOC course to be slapdash, unplanned, and in
many cases pure nonsense (link). I wound up personally corresponding with
Sebastian Thrun (Stanford professor, founder of Udacity, head of
Google's auto-car project) over it, and came away super skeptical of his
work. Today here's a fantastic article about the fallen hopes for MOOCs
and Thrun's Udacity in particular -- highly recommended, jealous that I
didn't write this.
Just a few short years after promising higher education for anyone with an Internet connection, MOOCs have scaled back their ambitions, content to become job training for the tech sector and for students who already have college degrees...I want to quote the whole thing here; probably best that you just go and read it. Big kudos to Audrey Waters for writing this (and tip to Cathy O'Neil for sharing a link).
"In 50 years,” Thrun told Wired, “there will be only 10 institutions in the world delivering higher education and Udacity has a shot at being one of them.”
Three years later, Thrun and the other MOOC startup founders are now telling a different story. The latest tagline used by Thrun to describe his company: “Uber for Education.”
2015-08-24
On Registered Clinical Trials
A new PLoS ONE study looks at the effect of mandatory pre-registration of medical study methods and outcome measures, starting in 2000. Major findings:
- Studies finding positive effects fell from 57% prior to the registry to just 8% afterward.
- "...focused on human randomized controlled trials that were funded by the US National Heart, Lung, and Blood Institute (NHLBI) [and so required advanced registration by a 1997 U.S. law]. The authors conclude that registration of trials seemed to be the dominant driver of the drastic change in study results."
- "Steven Novella of Yale University in New Haven, Connecticut, called the study 'encouraging' but also 'a bit frightening' because it casts doubt on previous positive results...”
- "Many online observers applauded the evident power of registration and transparency, including Novella, who wrote on his blog that all research involving humans should be registered before any data are collected. However, he says, this means that at least half of older, published clinical trials could be false positives. 'Loose scientific methods are leading to a massive false positive bias in the literature,' he writes."
2015-08-16
Is Cohabitation Good for You?
Last week, Ars Technica (and I'm sure other news sites) posted an article on a large-scale survey of health outcomes in Britain, under the headline, "Good news for unmarried couples — cohabitation is good for you" (subtitle: "Married partners tend to be healthy, but living with someone works just as well"). Link.
I'm actually hyper-critical about people who sling around the phrase "correlation does not imply causation" too much in improper cases, but here's a golden example where it does apply; the headline "cohabitation is good for you", is totally unwarranted. Now, the findings do say that married & cohabiting people are healthier than people who live alone. But this could be either X causes Y, or Y causes X, or other more complicated interactions. One hypothesis is that "cohabitation is good for you [by improving health]"; another hypothesis is that "being healthy is good for your prospects of getting a partner", i.e., healthy people make for more attractive marriage/cohabitation partners. If you think about it, I'd say that the latter is actually the more common-sense direction of the causation here.
I'm actually hyper-critical about people who sling around the phrase "correlation does not imply causation" too much in improper cases, but here's a golden example where it does apply; the headline "cohabitation is good for you", is totally unwarranted. Now, the findings do say that married & cohabiting people are healthier than people who live alone. But this could be either X causes Y, or Y causes X, or other more complicated interactions. One hypothesis is that "cohabitation is good for you [by improving health]"; another hypothesis is that "being healthy is good for your prospects of getting a partner", i.e., healthy people make for more attractive marriage/cohabitation partners. If you think about it, I'd say that the latter is actually the more common-sense direction of the causation here.
2015-07-20
The Difference a Teacher Makes
I had an interesting natural experiment this past spring semester: I was teaching two remedial algebra courses, one in the afternoon, and one in the evening. Same calendar days, same class sizes, identical lectures from day to day, exact same tests, exact same numbers taking the final exam. In one class, only 23% of the registrants passed the final exam, while in the other class 60% passed. (Median scores on the final were 48% in one class and 80% in the other.)
This got me to wondering: How much difference does the teacher make in these classes? And the honest answer is: not very much. To be humble about it, I could do everything humanly possible both inside and outside the classroom as a teacher, work at maximal effort all the time (and that is generally my goal), and have it make very little difference in the overall classroom result. The example here of enormous variation between two sections, identically treated by me as an instructor, really highlights this fact.
On this point, I found a 2013 paper from ETS by Edward H. Haertel -- principally about the unreliability of teacher VAM scores -- that summarizes several studies as finding that the difference in test scores attributable to teacher proficiency is only about 10% (see p. 5). That actually seems about right based on my recent experiences.
This got me to wondering: How much difference does the teacher make in these classes? And the honest answer is: not very much. To be humble about it, I could do everything humanly possible both inside and outside the classroom as a teacher, work at maximal effort all the time (and that is generally my goal), and have it make very little difference in the overall classroom result. The example here of enormous variation between two sections, identically treated by me as an instructor, really highlights this fact.
On this point, I found a 2013 paper from ETS by Edward H. Haertel -- principally about the unreliability of teacher VAM scores -- that summarizes several studies as finding that the difference in test scores attributable to teacher proficiency is only about 10% (see p. 5). That actually seems about right based on my recent experiences.
Reliability and Validity of Inferences About Teachers Based on Student Test Scores
2015-06-08
Why Technology Won't Fix Schools
Kentaro Toyama is a professor at U. Michigan, a fellow at MIT, and a former researcher for Microsoft. He's just written a book titled "Geek Heresy: Rescuing Social Change from the Cult of Technology" (although I'd quibble with the title in one way: practically all geeks I know consider the following to be obvious and common-sense). He writes:
And, oh, how much do I agree with the following!:
More at the Washington Post (link).
But no matter how good the design, and despite rigorous tests of impact, I have never seen technology systematically overcome the socio-economic divides that exist in education. Children who are behind need high-quality adult guidance more than anything else. Many people believe that technology “levels the playing field” of learning, but what I’ve discovered is that it does no such thing.
And, oh, how much do I agree with the following!:
... what I’ve arrived at is something I think of as technology’s Law of Amplification: Technology’s primary effect is to amplify human forces. In education, technologies amplify whatever pedagogical capacity is already there.
More at the Washington Post (link).
2015-06-01
Noam Chomsky on Corporate Colleges
Noam Chomsky speaks on issues of non-teaching administrators taking over America's colleges, the use of part-time and non-governing faculty, and related issues:
The university is probably the social institution in our society that comes closest to democratic worker control. Within a department, for example, it’s pretty normal for at least the tenured faculty to be able to determine a substantial amount of what their work is like: what they’re going to teach, when they’re going to teach, what the curriculum will be. And most of the decisions about the actual work that the faculty is doing are pretty much under tenured faculty control.More at Salon.com.
Now, of course, there is a higher level of administrators that you can’t overrule or control. The faculty can recommend somebody for tenure, let’s say, and be turned down by the deans, or the president, or even the trustees or legislators. It doesn’t happen all that often, but it can happen and it does. And that’s always a part of the background structure, which, although it always existed, was much less of a problem in the days when the administration was drawn from the faculty and in principle recallable.
Under representative systems, you have to have someone doing administrative work, but they should be recallable at some point under the authority of the people they administer. That’s less and less true. There are more and more professional administrators, layer after layer of them, with more and more positions being taken remote from the faculty controls.
2015-05-25
Online Courses Fail at Community Colleges
More evidence for one of the most uniformly-verified findings I've seen in education: online courses strike out for community college students. From a paper by researchers at U.C.-Davis, presented at the American Educational Research Association's conference in April:
“In every subject, students are doing better face-to-face,” said Cassandra Hart, one of the paper’s authors. “Other studies have found the same thing. There’s a strong body of evidence building up that students are not doing quite as well in online courses, at least as the courses are being designed now in the community college sector.”More at Alternet.org.
2015-05-18
Teaching Evolution in Kentucky
A professor discusses teaching evolution in Kentucky. "Every time a
student stomps out of my auditorium slamming the door on the way, I
can’t help but question my abilities." (Link.)
(Thanks to Jonathan Scott Miller for the link.)
(Thanks to Jonathan Scott Miller for the link.)
2015-05-11
On Definitions
From the MathBabe blog by poster EllipticCurve, here:
Mathematical definitions mean nothing until you actually use them in anger, i.e. to solve a problem...
2015-05-04
Quad Partners Buys Inside Higher Ed
From Education News in January:
Although there has been no public announcement made, Quad Partners, a New York private equity firm devoted to the for-profit college industry, recently gained a controlling stake in the education trade publication Inside Higher Ed (IHE). The publication routinely reports on for-profit colleges and surrounding policy disputes, and the publication is now listed among investments on the Quad Partners website.Read more here.
2015-04-27
ETS on Millennials
A fascinating report on international education and job-ready skills from the Educational Testing Service. Particularly so, as it almost directly impinges on committee work that I've been doing lately. Core findings:
See the online report here.
- While U.S. millennials have far higher degree certifications than prior generations, their literacy, numeracy, and use-of-technology skills are demonstrably lower.
- U.S. millennials rank 16th of 22 countries in literacy. They are 20th of 22 in numeracy. They are tied for last in technology-based problem solving.
- Numeracy for U.S. millennials has been dropping across all percentiles since at least 2003.
See the online report here.
2015-04-20
Causes of College Cost Inflation
From testimony at Ohio State (link):
- Decreased state funding
- Administrative bloat
- Cost of athletics
2015-04-13
Pupils Prefer Paper
You may have already seen this article on the work of Naomi S. Baron at American University: her studies show that for textbook-style reading and studying, young college students still prefer paper books over digital options. Why? Because of reading.
Read the article at the Washington Post.
In years of surveys, Baron asked students what they liked least about reading in print. Her favorite response: “It takes me longer because I read more carefully.”...
Another significant problem, especially for college students, is distraction. The lives of millennials are increasingly lived on screens. In her surveys, Baron writes that she found “jaw-dropping” results to the question of whether students were more likely to multitask in hard copy (1 percent) vs. reading on-screen (90 percent).
Read the article at the Washington Post.
2015-04-06
Academically Adrift Again
One more time, as we've pointed out here before (link), in this case from Jonathan Wai of Duke University: "the rank order of cognitive skills of various
majors and degree holders has remained remarkably constant for the last
seven decades", with Education majors perennially the very lowest of performers (closely followed by Business and the Social Sciences).
See Wai's article and charts here.
See Wai's article and charts here.
2015-03-30
Newtonian Weapons
The ponderous instrument of synthesis, so effective in Newton's hands, has never since been grasped by anyone who could use it for such purpose; and we gaze at it with admiring curiosity, as some gigantic implement of war, which stands idle among the memorials of ancient days, and makes us wonder what manner of man he was who could wield as a weapon what we can hardly lift as a burden.- William Whewell on Newton’s geometric proofs, 1847 (thanks to JWS for pointing this out to me).
2015-03-23
Average Woman's Height
A quick observation: statements like "the average woman's height is 64 inches" are almost always misinterpreted. Here's the main problem: people think that this is referencing an archetypal "average woman", when it's not.
The proper parsing is not "the (average woman's) height"... but it is "the average (woman's height)". See the difference? It's really a statement about the variable "woman's height", which has been measured many times, and then averaged. In short, it's not about an "average woman", but rather an "average height" (of women).
Of course, this misunderstanding is frequently intentionally mined for comedy. See yesterday's SMBC comic (as I write this), for example: here.
The proper parsing is not "the (average woman's) height"... but it is "the average (woman's height)". See the difference? It's really a statement about the variable "woman's height", which has been measured many times, and then averaged. In short, it's not about an "average woman", but rather an "average height" (of women).
Of course, this misunderstanding is frequently intentionally mined for comedy. See yesterday's SMBC comic (as I write this), for example: here.
2015-03-16
Identifying Proportions Proposal
Let me again ask the question, "How Do You Know Something is a Proportion?". For the math practitioner this is one of those things that requires no explanation ("you just know", "it's just common sense"). But for the remedial college algebra student, running into these common questions on tests, it's a real stumbling block to recognize when the proportional exercise is being asked. Actually, I've found that it's a stunningly hard problem to explain when we know something is proportional -- I've asked the question online twice here (first, second), I've asked around to friends, and rarely do I get any really coherent answer back at all. (One professor colleague investigated the issue and then said, "It's the question on the final that doesn't have a clear direction to it, that's how you know."). Any college basic-math textbook I look at has a stunningly short attempt at a non-explanation, as though they're keenly embarrassed that they really can't explain it at all (usually in the form of, "Proportions are useful, for example in the following cases..."; see first link above for specifics). Let's see if we can do better this week.
Proportions in the Common Core
First, let's look at what the up-and-coming Common Core curriculum does with this issue. In CC ratios and proportions are a 7th-grade topic, and there is a presentation specifically on the subject of "identifying proportions". This is uniformly given by two methods: (1) a table of paired numbers, and (2) a graph of a relationship. The key in the first case is to see that the pairs of numbers are always related by the same multiplication factor (usually a simple integer), i.e., y = kx. In the second case you're looking for a straight line that goes through the origin (0, 0), which I think is not a bad tactic. These materials very consciously avoid relying on the cross-multiplying ratios trick, and seek instead to develop a more concrete intuition for the relationship. I think that's a pretty solid methodology actually, and I've come to agree that the common cross-product way of writing these obscures the actual relationship (see also work like Lesh, 1988 that argues similarly).Some references to Common Core materials where you see this strategy in play:
In College Remedial Courses
Second, let's observe that the exercises and test questions in our remedial algebra classes at the college level are not given in this format of numerous-data-points; rather, a much more cursory word problem is stated. In fact, let us admit that most of our exercises are at least somewhat malformed -- they are ambiguous, they require some background assumption or field-specific knowledge that things are proportional; they fail to be well-defined in an almost unique way. Here are a few examples from Elayn Martin-Gay's otherwise excellent Prealgebra & Introductory Algebra, 3rd Edition (2011), Section 6.1:49. A student would like to estimate the height of the Statue of Liberty in New York City's harbor. The length of the Statue of Liberty's right arm is 42 feet. The student's right arm is 2 feet long and her height is 5 1/3 feet. Use this information to estimate the height of the Statue of Liberty.Notice that this doesn't assert that the person and the statue are proportional. In fact I can think of a lot of artistic, structural, or biological reasons why it wouldn't be. In this way the problem is not really well-defined.
51. There are 72 milligrams of cholesterol in a 3.5-ounce serving of lobster. How much cholesterol is in 5-ounces of lobster? Round to the nearest tenth of a milligram.As someone who's eaten a lot of cheap lobster growing up in Maine, again I can think of a lot of reasons of why the nutritional meat content of lobster might not be proportional across small and large lobsters (the basic serving being one creature of whatever size). For example, the shell hardness is very different across different sizes.
57. One out of three American adults has worked in the restaurant industry at some point during his or her life. In an office of 84 workers, how many of these people would you expect to have worked in the restaurant industry at some point?My immediate guess would be: definitely less than one-third of the office. It seems that a sample of current office workers are somewhat more likely to have worked in an office all their career and therefore (thinking from the standpoint of statistical inference) fewer of them would have worked in a restaurant than the broad population. For example, simply change the word "office" here to "restaurant" and the answer is clearly not one-third (specifically it would be 100%), cluing us into the fact that former restaurant workers are not spread around homogeneously.
I don't really mean to pick on Martin-Gay here, because many of her other exercises in the same section avoid these pitfalls. The very next exercise on the Statue of Liberty says, "Suppose your measurements are proportionally the same...", the one on skyscraper height says, "If the Empire State Building has the same number of feet per floor...", others give the mixture "ratio" or medication dose "for every 20 pounds", all of which nicely serve to solve the problem and make them well-defined.
But I've seen much worse perpetrated by inattentive professors in their classrooms, tests, and custom books. So even if Martin-Gay fixes all of her exercises precisely, plenty of instructors will surely continue to overlook the details, and continue to assume their own background contextual knowledge in these problems that their remedial students simply don't have. In short, for some reason, we as a professorship continually keep writing malformed and poorly-defined problems that secretly rely on our application background knowledge of things as proportional.
Proposed Solution
Here's the solution that I've decided to try this semester in my remedial algebra courses. To start with, I'll try to draw a direct connection to the Common Core exercises, such that if someone ever has or does encounter that, hopefully some neurons will recognize the topic as familiar. Instead of saying that a proportion is an equality of ratios (as most of these college books do), I will instead say that it's a "relation involving only a multiply/divide", emphasizing the essential simplicity of the relation (really just one kind of operation; no add/subtracts or exponents/radicals), and covering the expression of it as either y = kx or a/b = c/d.The hope here is that we can then intuit in different cases, asking, "does this seem like a simple multiply operation?", with the supplemental hint (stolen from Common Core), "would zero result in zero?". For example: (a) paint relating to surface area (yes; zero area would require zero paint), (b) weight and age (no; a zero-age child does not weigh zero pounds). In addition -- granted that students will be certain to encounter these frankly malformed problems -- I will list some specific contextual examples, that will show up in exercises and tests, to try to full in the gap of application-area knowledge that many of us take for granted. Here's what my brief lecture notes look like now:
Proportions: Relations involving only multiply/divide (also: “direct variation”). Examples: Ingredients in recipes, gas consumption, scale comparisons. (Hint: Does 0 give 0?). Formula: a/b = c/d, where a & c share units, and so do b & d. Ex.: If 2 boxes of cereal cost $10, then how much do 6 boxes cost? 10/2 = x/6 → 60 = 2x → 30 = x. Interpret: 6 boxes cost $30. Ex.: (YSB4, p. 68) 22; 24. [4/7 = 12/x. Interpret: 12 marbles weigh 21 grams.]
So that's what I'll be trying out in my courses this week. We'll see how it goes; at least I think I have a legitimate answer now when a student asks for these kinds of problems, "but how do we know it's proportional?".
2015-03-14
Pi Proofs for the Area of a Circle
For Half-Tau Day: Approximately π short proofs for the area of a circle, each in terms of τ = 2π (that is, one "turn"), mostly using calculus.
Shells in Rectangular Coordinates
See the first picture above. Imagine slicing the disk into very thin rings, each with a small width ds, at a radius of s, for a corresponding circumference of τs (by definition of τ). So each ring is close to a rectangle if straightened out, with length τs and a width of ds, that is, close to an area of τs ds. In the limit for all radii 0 to r, this gives:Sectors in Polar Coordinates
See the second picture above. Imagine slicing the disk into very thin wedges, each with a small radian angle dθ and a corresponding arclength of r dθ (by definition of θ). So each wedge is close to a triangle (half a rectangle) with base r and a height of r dθ, that is, close to an area of r²/2 dθ. In the limit for all angles 0 to τ, this gives:Unwrapping a Triangle
Sort of taking half of each of the ideas above, we can geometrically "unwrap" the rings in a circle into a right triangle. One radius stays fixed at height r. The outermost rim of the circle becomes the base of the triangle, with width as the circumference τr. So the area of this triangle is:Comments
The interesting thing about the first two proofs is that between them they interchange the radius r and the circle constant τ in the bounds versus the integrand. The interesting thing about the last demonstration is that it matches the phrasing of Archimedes' original, pre-algebraic conclusion: the area of a circle is equal to that of a triangle with height equal to the radius, and base equal to the circumference (proven with more formal geometric methods).Of course, if you replace τ in the foregoing with 2π, then the multiply-and-divide by 2's cancel out, and you get the more familiar expression πr². But I actually like seeing the factor of r²/2 in the version with τ, as both foreshadowing and reminder that ∫ r dr = r²/2, and also that it's half of a certain rectangle (as I might paraphrase Archimedes). In addition, Michael Hartl makes the point that this matches a bunch of similar basic formulas in physics (link).
Thanks to MathCaptain.com and Wikipedia for the images above.
2015-03-09
Vive la Différence?
A colleague of mine says that he wants to spend time giving his students more video and I equivocate in my response. He presses the question: "Don't you agree that different people learn in different ways?"
Here's one possibly reply. First, to my understanding there's no evidence that trying to match delivery to different "learning styles" has any positive effect on outcomes. One example I came across yesterday: a Department of Education meta-analysis of thousands of studies found no learning evidence of benefits from online videos ("Elements such as video or online quizzes do not appear to influence the amount that students learn in online classes.", p. xvi, here). Perhaps the short version of this response would be, "Not in any way that makes a significant difference."
But here's another possible response, to answer the question with another question: "Don't you agree that it's important to have a shared, common language for communication in any field?" And as usual I would argue that acting like math, or computer programming is anything other than essentially a written artifact is fallacious -- in fact, overlooking the fact that writing in general is the most potent tool ever developed in our arsenal as human beings (including factors such as brevity, density, speed, searchability, auditability, etc.) is fallacious, a fraud, a failure.
To the extent that we delay delivering and practicing the "real deal" for our students -- namely, properly-written math -- it is a tragic garden path.
Here's one possibly reply. First, to my understanding there's no evidence that trying to match delivery to different "learning styles" has any positive effect on outcomes. One example I came across yesterday: a Department of Education meta-analysis of thousands of studies found no learning evidence of benefits from online videos ("Elements such as video or online quizzes do not appear to influence the amount that students learn in online classes.", p. xvi, here). Perhaps the short version of this response would be, "Not in any way that makes a significant difference."
But here's another possible response, to answer the question with another question: "Don't you agree that it's important to have a shared, common language for communication in any field?" And as usual I would argue that acting like math, or computer programming is anything other than essentially a written artifact is fallacious -- in fact, overlooking the fact that writing in general is the most potent tool ever developed in our arsenal as human beings (including factors such as brevity, density, speed, searchability, auditability, etc.) is fallacious, a fraud, a failure.
To the extent that we delay delivering and practicing the "real deal" for our students -- namely, properly-written math -- it is a tragic garden path.
2015-03-02
More Studies that Tech Handouts Hurt Students
From an Op-Ed in the New York Times on 1/30/15 by Susan Pinker, a developmental psychologist:
Read more here.
In the early 2000s, the Duke University economists Jacob Vigdor and Helen Ladd tracked the academic progress of nearly one million disadvantaged middle-school students against the dates they were given networked computers. The researchers assessed the students’ math and reading skills annually for five years, and recorded how they spent their time. The news was not good.
“Students who gain access to a home computer between the 5th and 8th grades tend to witness a persistent decline in reading and math scores,” the economists wrote, adding that license to surf the Internet was also linked to lower grades in younger children.
In fact, the students’ academic scores dropped and remained depressed for as long as the researchers kept tabs on them. What’s worse, the weaker students (boys, African-Americans) were more adversely affected than the rest. When their computers arrived, their reading scores fell off a cliff.
Read more here.
2015-02-23
Conic Sections in Play-Doh
Here's an idea for illustrating all the different shapes you can get out of conic sections: get some Play-Doh, roll it out into a cone shape (the "conic" part) -- and also a reasonably sharp knife (for the "sections" part).
First, here's our starting cone:
Note that if you cut off just the tippy-top part then you get a single point:
On the other hand, if you carefully take a shaving down the very edge then it produces a line:
But if you make a slice perpendicular to the base, then you get a perfect circle (of any size you want, depending on how far down the cone you take it):
Make a similar slice at a slight angle and the cross-section you get is now an ellipse:
Take the slice at a steeper angle and you'll produce our old quadratic friend, the parabola:
And increase the angle a bit more (greater than the edge of the cone itself), and you'll produce the parabola's angry cousin, the hyperbola (or really a half-branch of such):
Kind of neat. Full disclosure: the cone gets pretty "smooshed" on each cut (kind of like a loaf of bread with a dull knife), and I had to gently re-shape back into the proper section before each photo. Therefore, this demonstration probably works best in static photography, and would be somewhat less elegant live or in a video. But the nice thing about the Play-Doh is that you can sticky it back together pretty well after each sectional cut, and it's the only material I could think of that would work well in that way. Can you think of anything else?
First, here's our starting cone:
Note that if you cut off just the tippy-top part then you get a single point:
On the other hand, if you carefully take a shaving down the very edge then it produces a line:
But if you make a slice perpendicular to the base, then you get a perfect circle (of any size you want, depending on how far down the cone you take it):
Make a similar slice at a slight angle and the cross-section you get is now an ellipse:
Take the slice at a steeper angle and you'll produce our old quadratic friend, the parabola:
And increase the angle a bit more (greater than the edge of the cone itself), and you'll produce the parabola's angry cousin, the hyperbola (or really a half-branch of such):
Kind of neat. Full disclosure: the cone gets pretty "smooshed" on each cut (kind of like a loaf of bread with a dull knife), and I had to gently re-shape back into the proper section before each photo. Therefore, this demonstration probably works best in static photography, and would be somewhat less elegant live or in a video. But the nice thing about the Play-Doh is that you can sticky it back together pretty well after each sectional cut, and it's the only material I could think of that would work well in that way. Can you think of anything else?
2015-02-16
Sorting Blackboard Test Results
On the Blackboard class management system, tests may be assigned where the order of the questions is randomized for different students (useful to somewhat improve security, make sure no question is biased due to ordering, etc.). However, a problem arises: when individual results are downloaded, the questions still appear in this randomized order for each separate student. That is: questions don't match down columns, they don't match in the listed "ID" numbers, etc.; and therefore there's no obvious way to assess or correlate individual questions between students or with any outside data source (such as a final exam, pretest/post-test structure, etc.). A brief discussion about this problem can be found on the "Ask the MVP" forum on the Blackboard site (link).
Now here's a solution: I wrote a computer application to take downloaded Blackboard results in this situation and sort them back into consistent question ordering, and thereby make them usable for correlation analysis (in a spreadsheet, SPSS, etc.). Java executable JAR file is below, first download that. Test results should be downloaded from Blackboard as a comma-delimited CSV file in the "long download" format ("by question and user" in the Blackboard Download Results interface), in the same directory (save as default "downloadlong.csv"). Then, on the command line, run the JAR file on by typing "java -jar BlackboardResultSort.jar".
The program reads the downloaded data file and outputs two separate files. The first, "questions.csv", is a key to the questions, listing each Question ID, Possible Points, and full Question text. The second, "users.csv", is a matrix of the different users (test-takers) and their scores on each question (each row is one user, and each column is their score for one particular question, consistent as per the questions.csv key). This makes it far more convenient to add outside data correlate success on any particular question with overall results. Ping me here if you have other questions.
Now here's a solution: I wrote a computer application to take downloaded Blackboard results in this situation and sort them back into consistent question ordering, and thereby make them usable for correlation analysis (in a spreadsheet, SPSS, etc.). Java executable JAR file is below, first download that. Test results should be downloaded from Blackboard as a comma-delimited CSV file in the "long download" format ("by question and user" in the Blackboard Download Results interface), in the same directory (save as default "downloadlong.csv"). Then, on the command line, run the JAR file on by typing "java -jar BlackboardResultSort.jar".
The program reads the downloaded data file and outputs two separate files. The first, "questions.csv", is a key to the questions, listing each Question ID, Possible Points, and full Question text. The second, "users.csv", is a matrix of the different users (test-takers) and their scores on each question (each row is one user, and each column is their score for one particular question, consistent as per the questions.csv key). This makes it far more convenient to add outside data correlate success on any particular question with overall results. Ping me here if you have other questions.
2015-02-02
Yitang Zhang Article in the New Yorker
The lead article in this week's New Yorker (Feb-2, 2015) is on Yitang Zhang, the UNH professor who appeared from obscurity last year to prove the first real result in the direction of the twin-primes conjecture (specifically, a concrete repeating bounded gap between primes; full article here).
To some extent I feel an unwarranted amount of closeness to this story. First, I grew up very close to UNH (just over the border in Maine), I would use the library there all through high school to do research for papers, and I worked at the dairy facility there for a few summers while I was in college. Secondly, the "twin primes conjecture" is basically the only real math research problem that I ever even had any intuition about -- along about senior year in my math program I think wrote a paper in abstract algebra where after some investigation on a computer I wrote "it's interesting to note that primes separated by only two repeat infinitely", to which the professor wrote back in red pen, "unproven conjecture!". I sort of have a running debate with a colleague at school that it's sort of intuitively obvious if you look at it, while course there's no rigorous proof. Yet.
When I saw this New Yorker in our apartment around midnight Friday after I got back from school, I first noticed that there was some article on math (the writer makes it pretty opaque initially about exactly who or what the subject is). My partner Isabelle immediately said, "For god's sake, don't read it tonight and go to bed angry!", to which I said, "Mmmm-hmmm, probably a good idea." But I did so anyway. Frankly, I got less angered by it than you might expect, because while it's big pile of dumb fucking shit, it's dumb in a way that so stupidly predictable it almost turns around and becomes comedy if you know what's going on. It's dumb in exactly the carbon-copy way, almost word-for-word that all of these articles are dumb -- so it's at least unsurprisingly stupid. Let's check off some boxes...
This is so goddamn predictable that, yes, it's the raison d'etre of this very six-year blog, to respond to that exact piece of nonsense in pop math writing (see tagline above; and the "Manifesto" in the first post). It's bullshit, it's not part of the real work of math. Sure, shorter is better, and it's far more convenient to get at a proof quickly with some heavy-caliber technique or clever trick, and I'd argue this is all that's meant by the "beautiful" trope. Someone gets careless and uses "beautiful" as a metaphor, in the way that Einstein or someone likes to pitch "God" as a metaphor -- when they secretly have some nonstandard definition like, "scientific research reducing superstition" (see: letter to Herbert Goldstein) -- and then it gets repeated by a thousand propagandists for their personal crusades. In the case of a pop media writer, they can latch onto the "beautiful" tag line and feel that they've got a hook on the story, and approach the rest of it like it's an article on Jeff Koons or some other high-society, celebrity scam artist.
But at any rate, the "beautiful math" pitch is entirely isolated to the article title and a single paragraph, it has zero connection to the rest of the story, it's basically just clickbait, so let's move on.
But here Wilkinson confronts a person who is ultimately patient, disciplined, humble, hard-working, and truth-seeking. And he doesn't know what the hell to do with that. No other professional mathematician had known what Zhang was doing for over 10 years. He received no accolades nor enemies. He doesn't seem aggrieved or jealous that other people's careers advanced ahead of his own. He speaks softly at awards ceremonies and talks. There's no "personal face" meat here.
So here's how Wilkinson responds; he makes the article about himself. Specifically about how he's a stupid damn bullshit artist. The opening paragraph is specifically about how apparently proud he is to know nothing about math, to be unqualified to write this story, and about how he's a fucking lying cheater:
Later, here's a summary of his interactions with Zhang:
This is not the kind of thing that a drinky, likely coke-blowing, social butterfly bullshit artist has any way of processing. And come on, that's pretty fucking funny; in that regard you almost couldn't make this stuff up. But on the downside it argues that these articles are always thricefold doomed; no journalist will ever write about the practice or results of math in any intelligible or useful way, because they're constitutionally, commercially, and philosophically opposed to it.
This is how predictable it all is: I give a mini-rant to Isabelle and she says, "Oh, he probably just went after something a family member mentioned to him once", and that is in fact exactly what motivated the article (see end of the first paragraph). So frankly I could read about three sentences and map out in advance the progression of all the rest of the article. Hard to get usefully enraged by that; just standard-stupid is all.
Unfortunately, this hits me something like an attack right through my own person. This is exactly the way that I personally failed in graduate school, and did not proceed on to the doctorate -- by continuing to work furiously in isolation while the rest of the classes basically passed me by. I've recently seen this called "John Henry Disease" in the work of Claude Steele (although there he holds it out as uniquely a phenomenon for black students). When I bring this up to colleagues nowadays, I can tell this story lightly enough that I get a laugh out of them, "Obviously you had to know better than that", or some-such. But a combination of personality and cultural upbringing literally left me completely unaware of the idea that you'd go get someone else's help on a math problem. So in that regard the "math community" thesis is a strong one.
But on the other hand, the whole prime-directive that I've established for my math classes in the last few years is: Learn how to read and write math properly. It's literally the first thing on my syllabi now; the idea that math (algebraic) language is inherently a written language and not primarily verbal, and that this is the hard thing to master if you're a standard poorly-prepared city public high school graduate. That learning to read a math book was the key that got me through calculus and all the rest of a math program (through the undergraduate level, anyway). That the software that runs our world are fundamentally products of writing (see a prior post here). And once I commit to this goal in class, and get most of the students to buy in to it, I've been getting what I think are wonderful and satisfying results with it, incredibly encouraging, in the last few years. Ken Bain's book "What the Best College Teachers Do" hits on this as an even more universal theme: "We found among the most effective teachers a strong desire to help students learn to read in the discipline." (Chapter 3, item #8).
And now here we have, in the very recent past, multiple cases of major mathematical breakthroughs by people working entirely in isolation, effectively in secret, for one to two decades, interacting only with the published literature in the field and their own brainpower. This is what's held out as Zhang's experience. And the same could be said for Perelman with the Poincaré conjecture, right? And also Andrew Wiles with Fermat's Last Theorem. And maybe Shinichi Mochizuki with the abc conjecture? (Here's where the argument rages.) A common theme recently is that with ever-more stringent publishing requirements for tenure, people on the standard academic track must publish every year or two, not meditate on the deepest problems for a decade. And so does the institution actually force isolation on the people tackling these giant problems? Or is it merely the nature of the beast itself?
An aside: I have this exact same issue in terms of my gaming work with Dungeons & Dragons (see that blog here). The conventional wisdom is "obviously we all know that no one could learn D&D on their own, we all had some older mentor(s) who inducted us into the game". And I am in the very rare situation for whom that is absolutely false. Growing up in a rural part of Maine, the only reason I ever heard about the game was through magazines; I was the first person to get the rulebooks and read them; and the catalyst in my town and school, among anyone I ever knew, to introduce and run the game for them. Purely from the written text of the rulebooks. To the extent that there were any other conventions or understandings about the game that didn't get into the books, I never knew about them. Which in retrospect has been both a great strength and in some fewer cases a weakness for me. In short: I learned purely from the book and most people don't believe that's possible.
But back to the article by Wilkinson: he expresses further dismay and incredulity at Zhang's solitary existence, his disinterest in social gatherings, and his preference for taking a bus to school so that he can get more thinking time in. All things which I could say pretty much identically for myself; and all things which our standard-template journalist is going to find alien and utterly bewildering:
But those are just nit-picky details, and we've probably already given the article writer more attention than he deserves. Let me finish by addressing the elephantine angel in the room. Are the true, greatest breakthroughs really made by loners, working in isolation with just the written text, over decades of time? Or is that just another journalistic illusion?
To some extent I feel an unwarranted amount of closeness to this story. First, I grew up very close to UNH (just over the border in Maine), I would use the library there all through high school to do research for papers, and I worked at the dairy facility there for a few summers while I was in college. Secondly, the "twin primes conjecture" is basically the only real math research problem that I ever even had any intuition about -- along about senior year in my math program I think wrote a paper in abstract algebra where after some investigation on a computer I wrote "it's interesting to note that primes separated by only two repeat infinitely", to which the professor wrote back in red pen, "unproven conjecture!". I sort of have a running debate with a colleague at school that it's sort of intuitively obvious if you look at it, while course there's no rigorous proof. Yet.
When I saw this New Yorker in our apartment around midnight Friday after I got back from school, I first noticed that there was some article on math (the writer makes it pretty opaque initially about exactly who or what the subject is). My partner Isabelle immediately said, "For god's sake, don't read it tonight and go to bed angry!", to which I said, "Mmmm-hmmm, probably a good idea." But I did so anyway. Frankly, I got less angered by it than you might expect, because while it's big pile of dumb fucking shit, it's dumb in a way that so stupidly predictable it almost turns around and becomes comedy if you know what's going on. It's dumb in exactly the carbon-copy way, almost word-for-word that all of these articles are dumb -- so it's at least unsurprisingly stupid. Let's check off some boxes...
The "Beautiful Math" Trope
Sure enough, the title of the article is "The Pursuit of Beauty". Paragraph #2 of the article is a string of predictable quotes by some dead white guys about "proofs can be beautiful" (G.H. Hardy, Bertrand Russell). The writer managed to find one living professor who he got to use that word one time (Edward Frankel, UC Berkeley, the proof having "a renaissance beauty", sounding like the author pressed him on the question and was grudgingly humored). And then he gets a hail-Mary sentence on neuroscientists connecting math to art in some lobe of the brain. But Zhang never says that. Nor anyone else in the article from that point.This is so goddamn predictable that, yes, it's the raison d'etre of this very six-year blog, to respond to that exact piece of nonsense in pop math writing (see tagline above; and the "Manifesto" in the first post). It's bullshit, it's not part of the real work of math. Sure, shorter is better, and it's far more convenient to get at a proof quickly with some heavy-caliber technique or clever trick, and I'd argue this is all that's meant by the "beautiful" trope. Someone gets careless and uses "beautiful" as a metaphor, in the way that Einstein or someone likes to pitch "God" as a metaphor -- when they secretly have some nonstandard definition like, "scientific research reducing superstition" (see: letter to Herbert Goldstein) -- and then it gets repeated by a thousand propagandists for their personal crusades. In the case of a pop media writer, they can latch onto the "beautiful" tag line and feel that they've got a hook on the story, and approach the rest of it like it's an article on Jeff Koons or some other high-society, celebrity scam artist.
But at any rate, the "beautiful math" pitch is entirely isolated to the article title and a single paragraph, it has zero connection to the rest of the story, it's basically just clickbait, so let's move on.
Journalist-Mathematician Antimatter
The broader issue that makes article count as downright comedy is the completely predictable acid-and-water interaction between the journalist and the mathematician. The writer here, Alec Wilkinson, is an exemplar of his industry -- scammy, full of bullshit, and just downright really fucking stupid. We've all met these folks at this point, have we not? Doesn't really know about anything. Has a single journalistic move up his sleeve for every article: "put a human face on the story", make it personal, make it about the people, "how did X make you feel?". (Elsewhere in the magazine, another writer waxes nostalgic for the classic traditions of New Yorker staffers: "all the editors dressed up and out every night for dinner and a show... a shrine of exotic booze...", Talk of the Town).But here Wilkinson confronts a person who is ultimately patient, disciplined, humble, hard-working, and truth-seeking. And he doesn't know what the hell to do with that. No other professional mathematician had known what Zhang was doing for over 10 years. He received no accolades nor enemies. He doesn't seem aggrieved or jealous that other people's careers advanced ahead of his own. He speaks softly at awards ceremonies and talks. There's no "personal face" meat here.
So here's how Wilkinson responds; he makes the article about himself. Specifically about how he's a stupid damn bullshit artist. The opening paragraph is specifically about how apparently proud he is to know nothing about math, to be unqualified to write this story, and about how he's a fucking lying cheater:
I don’t see what difference it can make now to reveal that I passed high-school math only because I cheated. I could add and subtract and multiply and divide, but I entered the wilderness when words became equations and x’s and y’s. On test days, I sat next to Bob Isner or Bruce Gelfand or Ted Chapman or Donny Chamberlain—smart boys whose handwriting I could read—and divided my attention between his desk and the teacher’s eyes.
Later, here's a summary of his interactions with Zhang:
Zhang is deeply reticent, and his manner is formal and elaborately polite. Recently, when we were walking, he said, “May I use these?” He meant a pair of clip-on shades, which he held toward me as if I might want to examine them first. His enthusiasm for answering questions about himself and his work is slight. About half an hour after I had met him for the first time, he said, “I have a question.” We had been talking about his childhood. He said, “How many more questions you going to have?” He depends heavily on three responses: “Maybe,” “Not so much,” and “Maybe not so much.” From diffidence, he often says “we” instead of “I,” as in, “We may not think this approach is so important.”... Peter Sarnak, a member of the Institute for Advanced Study, says that one day he ran into Zhang and said hello, and Zhang said hello, then Zhang said that it was the first word he’d spoken to anyone in ten days.
This is not the kind of thing that a drinky, likely coke-blowing, social butterfly bullshit artist has any way of processing. And come on, that's pretty fucking funny; in that regard you almost couldn't make this stuff up. But on the downside it argues that these articles are always thricefold doomed; no journalist will ever write about the practice or results of math in any intelligible or useful way, because they're constitutionally, commercially, and philosophically opposed to it.
This is how predictable it all is: I give a mini-rant to Isabelle and she says, "Oh, he probably just went after something a family member mentioned to him once", and that is in fact exactly what motivated the article (see end of the first paragraph). So frankly I could read about three sentences and map out in advance the progression of all the rest of the article. Hard to get usefully enraged by that; just standard-stupid is all.
The Community of Math
That said, the article does brush up against a real essential issue that I've been wrestling with for a few years now. Many of the math blogs that I've been reading in the last half-decade make a powerful and sustained case for the "community of math", that math cannot be done in isolation, that it only exists in the context of communicating with colleagues. Even that the writing of papers is inherently a peripheral and transient distraction, that the "true" productive activity of math is done verbally face-to-face and via body language with other experts -- writing being a faint shadow of that true work. (Hit me up for references on any of these points if you want them.)Unfortunately, this hits me something like an attack right through my own person. This is exactly the way that I personally failed in graduate school, and did not proceed on to the doctorate -- by continuing to work furiously in isolation while the rest of the classes basically passed me by. I've recently seen this called "John Henry Disease" in the work of Claude Steele (although there he holds it out as uniquely a phenomenon for black students). When I bring this up to colleagues nowadays, I can tell this story lightly enough that I get a laugh out of them, "Obviously you had to know better than that", or some-such. But a combination of personality and cultural upbringing literally left me completely unaware of the idea that you'd go get someone else's help on a math problem. So in that regard the "math community" thesis is a strong one.
But on the other hand, the whole prime-directive that I've established for my math classes in the last few years is: Learn how to read and write math properly. It's literally the first thing on my syllabi now; the idea that math (algebraic) language is inherently a written language and not primarily verbal, and that this is the hard thing to master if you're a standard poorly-prepared city public high school graduate. That learning to read a math book was the key that got me through calculus and all the rest of a math program (through the undergraduate level, anyway). That the software that runs our world are fundamentally products of writing (see a prior post here). And once I commit to this goal in class, and get most of the students to buy in to it, I've been getting what I think are wonderful and satisfying results with it, incredibly encouraging, in the last few years. Ken Bain's book "What the Best College Teachers Do" hits on this as an even more universal theme: "We found among the most effective teachers a strong desire to help students learn to read in the discipline." (Chapter 3, item #8).
And now here we have, in the very recent past, multiple cases of major mathematical breakthroughs by people working entirely in isolation, effectively in secret, for one to two decades, interacting only with the published literature in the field and their own brainpower. This is what's held out as Zhang's experience. And the same could be said for Perelman with the Poincaré conjecture, right? And also Andrew Wiles with Fermat's Last Theorem. And maybe Shinichi Mochizuki with the abc conjecture? (Here's where the argument rages.) A common theme recently is that with ever-more stringent publishing requirements for tenure, people on the standard academic track must publish every year or two, not meditate on the deepest problems for a decade. And so does the institution actually force isolation on the people tackling these giant problems? Or is it merely the nature of the beast itself?
When Zhang wasn’t working [at a Subway sandwich shop], he would go to the library at the University of Kentucky and read journals in algebraic geometry and number theory. “For years, I didn’t really keep up my dream in mathematics,” he said...
When we reached Zhang’s office, I asked how he had found the door into the problem. On a whiteboard, he wrote, “Goldston-Pintz-Yıldırım”and “Bombieri-Friedlander-Iwaniec.” He said, “The first paper is on bound gaps, and the second is on the distribution of primes in arithmetic progressions. I compare these two together, plus my own innovations, based on the years of reading in the library.”
An aside: I have this exact same issue in terms of my gaming work with Dungeons & Dragons (see that blog here). The conventional wisdom is "obviously we all know that no one could learn D&D on their own, we all had some older mentor(s) who inducted us into the game". And I am in the very rare situation for whom that is absolutely false. Growing up in a rural part of Maine, the only reason I ever heard about the game was through magazines; I was the first person to get the rulebooks and read them; and the catalyst in my town and school, among anyone I ever knew, to introduce and run the game for them. Purely from the written text of the rulebooks. To the extent that there were any other conventions or understandings about the game that didn't get into the books, I never knew about them. Which in retrospect has been both a great strength and in some fewer cases a weakness for me. In short: I learned purely from the book and most people don't believe that's possible.
But back to the article by Wilkinson: he expresses further dismay and incredulity at Zhang's solitary existence, his disinterest in social gatherings, and his preference for taking a bus to school so that he can get more thinking time in. All things which I could say pretty much identically for myself; and all things which our standard-template journalist is going to find alien and utterly bewildering:
Zhang’s memory is abnormally retentive. A friend of his named Jacob Chi said, “I take him to a party sometimes. He doesn’t talk, he’s absorbing everybody. I say, ‘There’s a human decency; you must talk to people, please.’ He says, ‘I enjoy your conversation.’ Six months later, he can say who sat where and who started a conversation, and he can repeat what they said.”
“I may think socializing is a way to waste time,” Zhang says. “Also, maybe I’m a little shy.”
A few years ago, Zhang sold his car, because he didn’t really use it. He rents an apartment about four miles from campus and rides to and from his office with students on a school shuttle. He says that he sits on the bus and thinks. Seven days a week, he arrives at his office around eight or nine and stays until six or seven. The longest he has taken off from thinking is two weeks. Sometimes he wakes in the morning thinking of a math problem he had been considering when he fell asleep. Outside his office is a long corridor that he likes to walk up and down. Otherwise, he walks outside.
Conclusion
There are more things I could criticize -- For example, in the absence of anything useful to say, the author has to hang onto any dumb or tentative attempt at an analogy that anyone throws at him, and is really helpless to double-check or confirm any assessment with anyone else; he literally can't understand anything anyone says about the math, even when interviews multiple professors on the same subject. He refers to Terry Tao like he's just "some professor", not one of the brightest and clearest thinkers on the planet. He has a paragraph on pp. 27-27, running 40 lines on the page, simply listing every variety of "prime number" he could find defined on Wikipedia (probably) -- the most blatant attempt at bloating up the word count of an article I think I've ever seen. Of course, it's intended to make your eyes cross and seem opaque. The exact opposite of a mathematical discipline dedicated to clear and transparent explanations.But those are just nit-picky details, and we've probably already given the article writer more attention than he deserves. Let me finish by addressing the elephantine angel in the room. Are the true, greatest breakthroughs really made by loners, working in isolation with just the written text, over decades of time? Or is that just another journalistic illusion?
Subscribe to:
Posts (Atom)









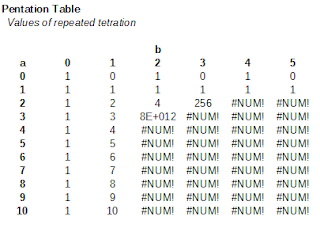


















How could the direction of this effect be formally disentangled? Well, you could be on the lookout for a "natural experiment" where someone who did manage to get married/cohabited breaks up or gets divorced, and see if their health degrades during the later period in which they lack a partner. Of course, the researchers here were smart enough to do exactly that, and an entire paragraph of the Ars Technica article is in fact devoted to these findings:
"The study found that changes in status had no obvious impact—the transitions from/to marriage and nonmarital cohabitation did not have a detrimental effect on health. There wasn’t an obvious difference in these biomarkers when participants divorced and then remarried or cohabitated; they looked the same as participants who remained married. For men who divorced in their late 30s and didn’t remarry, the risk of metabolic syndromes in midlife was reduced."
In other words, for anyone in the category of at least being healthy and attractive enough to get married/cohabited once, being married or cohabited made no difference to their health. Which to my eye is overwhelming evidence that the causation is in the other direction, i.e., these headlines of "cohabitation is good for you" are flat-out wrong.
Might be a good example to include in my fall statistics course.