NY Regents: Trivial to Pass

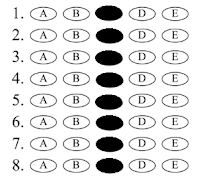
Ed Knight is a teacher in New York state. Writing at Medium, he points out the disturbing fact that the vaunted "New York Regents" exams required to graduate from high schools in the state have become completely trivial to pass. For example: In the Algebra Regents, you can ignore all of the (already simple) open-response questions, and just mindlessly mark "C" for all the multiple-choice questions, and you'll be given a passing grade.

Answer all Cs, you get 9 right. Each one is worth two points. That’s 18 points, enough to pass.

More than enough to pass, in fact.

I really didn’t know what to say when I first saw this. I suppose I was thinking like Chuck Heston. “They finally, really did it.” This is jaw-dropping malfeasance. I wouldn’t believe that anyone who claims to care about kids could let this happen — not until I saw it happen.

Shame on NYSED and the Regents.

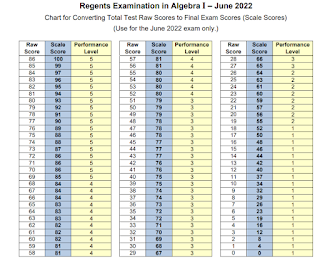
Really, the root of this problem is the insane scaling procedure that the NY Regents has been doing for years to fake up the test scores. Below is the most recent test's table for converting a "Raw Score to a reported "Scale Score". The scale score is 0-100, making recipients thinks it's a percentage, but it's not. For example: if you score a raw 27 out of the possible 86 points (that's 31% correct), this then gets converted to a reported Scale Score 65 -- i.e., a Performance Level of 3 out of 5, which is considered passing.

Think about that: for years, the NY Regents has considered a score of about 30% as passing for a basic (very simple!) algebra test. And yes, this was exacerbated because for the pandemic years (still ongoing), the policy was adjusted to accept even lower scores than that -- now as low as 20% (i.e., Raw 17, reported as a Scale 50). 

Read more at Medium: Guessing C For Every Answer Is Now Enough To Pass The New York State Algebra Exam

Curriculum in Califormia

A nicely comprehensive article late last year outlines the plans for the next overhaul of school mathematics curriculum in California -- delaying any algebra until high school, cutting and compressing later classes to fit the reduced time, disposing of gifted & talented or accelerated programs, de-tracking, etc. As usual, the motivation for this to hopefully see higher pass rates from the easier courses, claim to better support inequalities among minorities, be better positioned for well-paying STEM college programs and careers, etc. Among the fonts of battle are particularly academic math professors vs. math-education faculty, who are generally on opposing sides of the issue. 

One thing that really stuck out to me was the case of one student, who's held out as being the one black student throughout her advanced math courses in school, and currently studying as a math major at UC Berkley. Here's how her story is presented: 

Mariah Rose, a third-year applied math major at UC Berkeley, said she didn’t have another Black classmate in any of her math classes until this semester.

“There’s one other Black student in my class right now, and that’s just crazy to me,” said Rose. “The number of Black and Brown people in math is so low.”

Rose, who is half Black and half Latino, said this is nothing new. She said she was the only Black female student in her advanced math classes during high school. And her successes in math make her an outlier in California’s public school system where Black and Latino students score lower on standardized tests...

Rose, the UC Berkeley math major, said she has mixed feelings. She agrees with the framework’s recommendation to delay more advanced math classes and avoid labeling students based on their math abilities at younger ages. But she isn’t sure if she would be where she is if she hadn’t been accelerated into a higher-level math class in 6th grade. 

“It was a game changer,” she said. “I don’t know if I would’ve pursued math if I hadn’t advanced so early.”

Read the full article at The San Fransisco Standard.

Proofs and Applications

This is a quote that lives rent-free in my head, and comes up a lot in discussions I participate in.

From Stein/Barcellos, Calculus and Analytic Geometry, 5E, "To the Instructor", p. xxii (1992):

At the Tulane conference on "Lean and Lively Calculus" in 1986 we heard the engineers say, "Teach the concepts. We'll take care of the applications." Steve Whitaker, in the engineering department at Davis, advised us, "Emphasize proofs, because the ideas that go into the proofs are often the ideas that go into the applications." Oddly, mathematicians suggest that we emphasize applications, and the applied people suggest that we emphasize concepts. We have tried to strike a reasonable balance that gives the instructor flexibility to move in either direction.

Willingham on Automaticity

Some solid thoughts from Daniel Willingham on the need for automaticity in basic mathematics skills (re: automatic-algebra.org) from his article "Is It True That Some People Just Can't Do Math?" (American Educator, Winter 2009-2010):

In its recent report, the National Mathematics Advisory Panel argued that learning mathematics requires three types of knowledge: factual, procedural, and conceptual. Let’s take a close look at each.

Factual knowledge refers to having ready in memory the answers to a relatively small set of problems of addition, subtraction, multiplication, and division. The answers must be well learned so that when a simple arithmetic problem is encountered (e.g., 2 + 2), the answer is not calculated but simply retrieved from memory. Moreover, retrieval must be automatic (i.e., rapid and virtually attention free). This automatic retrieval of basic math facts is critical to solving complex problems because complex problems have simpler problems embedded in them. For example, long division problems have simpler subtraction problems embedded in them. Students who automatically retrieve the answers to the simple subtraction problems keep their working memory (i.e., the mental “space” in which thought occurs) free to focus on the bigger long division problem. The less working memory a student must devote to the subtraction subproblems, the more likely that student is to solve the long division problem.

This interpretation of the importance of memorizing math facts is supported by several sources of evidence. First, it is clear that before they are learned to automaticity, calculating simple arithmetic facts does indeed require working memory. With enough practice, however, the answers can be pulled from memory (rather than calculated), thereby incurring virtually no cost to working memory. Second, students who do not have math facts committed to memory must instead calculate the answers, and calculation is more subject to error than memory retrieval. Third, knowledge of math facts is associated with better performance on more complex math tasks. Fourth, when children have difficulty learning arithmetic, it is often due, in part, to difficulty in learning or retrieving basic math facts. One would expect that interventions to improve automatic recall of math facts would also improve proficiency in more complex mathematics. Evidence on this point is positive but limited, perhaps because automatizing factual knowledge poses a more persistent problem than difficulties related to learning mathematics procedures.

Get the whole article by Willingham (including citations for all the claims above) at the AFT website.

Remedial Equality Check

I discovered something last semester that made me insert a new little thing in the first day of my basic-level (remedial, liberal arts) community college math courses. A surprising proportion of my students are very confused about what the equality (=) sign means. 

Now, this isn't a tremendously novel observation, e.g., see: Baroody, Arthur J., and Herbert P. Ginsburg, "The effects of instruction on children's understanding of the 'equals' sign." The Elementary School Journal 84.2 (1983): 199-212. But the new discovery for me was how extremely simple a question it takes to make this visible. 

All I've done is start asking, "True or false? (a) 6 = 6, (b) 3 = 5". So far, everyone, confidently answers "true" to the first. But it seems like fully half of my students answer the second one incorrectly.

Last semester I had at least one or two students who were so enormously challenged that we could repeat this every day all semester and they'd never get it right. "True or false? 0 = 100"; "True"; "No, it's false"; "I don't get it". Over and over again every day, no matter how many times it was explained.

It seems pretty amazing, but there it is. Lots of our incoming community-college student literally don't now what the equals relation means. My best guess is that they've either come to think of it as "and here's the next thing", or that maybe instructors have been double-checking solutions to equations and every single time it's always come out true. 

I suppose it would be a decent research project to interview such students and ask them to explain what they think the equals sign means. Consider trying that for an opening exercise and share what your results are?