On Hyperoperations

Consider the basic operations: Repeated counting is addition; repeated addition is multiplication; repeated multiplication is exponentiation. Hyperoperations are the idea of generally extending this sequence. This was first proposed as such, in a passing comment, by R. L. Goodstein in an article to the Journal of Symbolic Logic, "Transfinite Ordinals in Recursive Number Theory" (1947):

At this point, there are a lot of different ways of denoting these operations. There's \(H_n\) notation. There's the Knuth up-arrow notation. There's box notation and bracket notation. The Ackerman function means almost the same thing. Conway's chained arrow notation can be used to show them. Some people concisely symbolize the zero-th level operation (under addition) as \(a \circ b\), and the fourth operation (above exponentiation) as \(a \# b\). Wikipedia reiterates Goodstein's original definition like so, for \(H_n (a,b): (\mathbb N_0)^3 \to \mathbb N_0\):

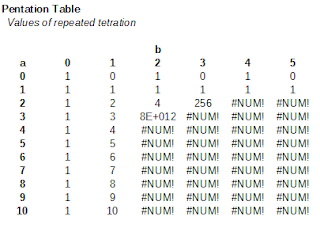
Let's use Goodstein's suggested names for the levels above exponentiation. Repeated exponentiation is tetration; repeated tetration is pentation; repeated pentation is hexation; and so forth. Since I don't see them anywhere else online, below you'll find some partial hyperproduct tables for these next-level operations (and ODS spreadsheet here). Of course, the values get large very fast; you'll see some entries in scientific notation, and then "#NUM!" indicates a place where my spreadsheet could no longer handle the value (that is, something greater than \(1 \times 10^{308}\)).

From this point forward, the hyperoperation tables look passingly similar in this limited view. You have some fixed values in the first two rows and columns; the 2-by-2 result is eternally 4; and everything other than that is so astronomically huge that you can't even usefully write it in scientific notation. Here are some identities suggested above that we can prove pretty easily for all hyperoperations \(n > 3\):

1. \(H_n(a, 0) = 1\) (by definition)
2. \(H_n(a, 1) = a\)
3. \(H_n(0, b) = \) 0 if b odd, 1 if b even
4. \(H_n(1, b) = 1\)
5. \(H_n(2, 2) = 4\)

One passingly interesting question is how many of these master identities hold true in the lower operations (n = 1 to 3; addition, multiplication, and exponentiation); in short, each step further down the hierarchy loses more of these identities, as summarized here:

Now, to connect up to my post last week, recall the basic properties of real numbers taken as axiomatic at the start of most algebra and analysis classes. Addition and multiplication (n = 1 and 2) are commutative and associative; but exponents are not, and neither are any of the higher operations.

Finally consider the general case of distribution, what in my algebra classes I summarize as the "General Distribution Rule" (Principle #2 here). Or perhaps based on last week's observation I might suggest it could be better phrased as "collecting terms of the next higher operation", like \(ac + bc = (a+b)c\) and \(a^c \cdot b^c = (a \cdot b)^c\), or in the general hyperoperational form: 

\(H_n(H_{n+1}(a, c), H_{n+1}(b, c)) = H_{n+1}(H_n(a, b), c)\)

Well, just like commutativity and associativity, distribution in this general form also holds for n = 1 and 2, but fails for higher operations. Here's the first counterexample, using \(a \uparrow b\) for exponents (\(H_3\)), and \(a \# b\) for tetration (\(H_4\)):

\((2\#2)\uparrow (0\#2) = 4 \uparrow 1 = 4\), but

\((2 \uparrow 0)\#2 = 1 \# 2 = 1\). 

Likewise, what I call the "Fundamental Rules of Exponents" (Principle #1 above, or also here) works only for levels \(n \le 3\), and fails to be meaningful at higher levels of hyperoperation.